Наивное решение за время O(nmk) предлагает делать следующее: положить всевозможные начальные положения робота в массив, а затем, в зависимости от текущей команды, сдвигать их в нужном направлении. На каждом шаге нужно проверять что все ли они находятся в клетке выхода.

Однако наивное решение не проходит по времени.

Авторское решение предполагает ускорение наивного решения при помощи битовых масок.

Все текущие положения робота будем хранить в прямоугольной битовой маске размера n × m. Маска поддерживает следующие операции:

1. Сдвиги влево, вправо, вверх, вниз.
2. Бинарные операции AND и OR.
3. Сравнение в другой маской.

Все эти операции можно реализовать так, чтобы они выполнялись за время O(nm / 32). Для реализации можно использовать массивы размера n × m / 32 или же std::bitset на C++.

Теперь, собственно, как моделировать весь процесс?

Сначала создадим маску base, в которой для каждой проходимой клетки стоит 1, а все остальные биты 0.

Создадим несколько дополнительных масок для каждого из четырех направлений: up1, up2, left1, left2, down1, down2, right1, right2. Маски с индексом 1 хранят клетки, которые находятся у стенки, а маски с индексом 2 хранят все остальные клетки маски base.

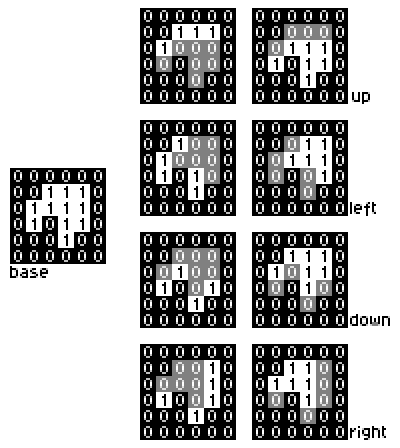
Кроме того, заведем еще маску, состоящую из одного бита в клетке выхода - маску E.

Теперь пусть все возможные текущие положения робота задаются маской T. Разобъем все эти положения на 2 подмножества - те, которые находятся у стенки и все остальные. Те, что не у стенки, подвинем в соответствии с текущей командой. Позиции у стенки не изменят своего положения. Теперь объединим два подмножества в одно и получим новую маску T. В виде выражения это выглядит так:

T = ((T and up1) or shift_up(T and up2));

Аналогичные выражения записываются для всех остальных направлений сдвига.

Теперь последовательно выполним все сдвиги, на каждом шагу сравнивая T с E. Как только они станут равны - следует вывести номер команды, после которое это произошло. Если равенства так и не случилось - нужно вывести -1.

Предложенное решение имеет сложность O(nmk / 32). Авторские решения на C++ и на Java без каких либо серьезных оптимизаций работают 0,9 с и 2,3 с соответственно.