Недавно в Голландии прошел subj. Результатов я пока не видел, но русские условия уже есть. Перепечатаю их сюда. Если кому-нибудь интересно, можно обсудить задачи. :)
Интересно, есть ли на codeforces участники IMO 2011? А прошлых лет?
- Для множества A = {a1, a2, a3, a4}, состоящего из четырех попарно различных целых положительных чисел, обозначим через sA сумму a1 + a2 + a3 + a4. Через nA обозначим количество пар индексов (i, j), 1 ≤ i < j ≤ 4, для которых sA делится на ai + aj. Найдите все множества A, состоящие из четырех попарно различных целых положительных, для которых nA принимает наибольшее возможное значение.
- Пусть S - конечное множество точек на плоскости, содержащее хотя бы две точки. Известно, что никакие три точки множества S не лежат на одной прямой. Назовем мельницей следующий процесс. Вначале выбирается прямая
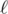 , на которой лежит ровно одна точка
, на которой лежит ровно одна точка 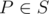 . Прямая
. Прямая 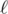 вращается по часовой стрелке вокруг центра P до тех пор, пока она впервые не пройдет через другую точку множества S. В этот момент эта точка, обозначим ее Q, становится новым центром, и прямая продолжает вращаться по часовой стрелке вокруг точки Q до тех пор, пока она снова не пройдет через точку множества S. Этот процесс продолжается бесконечно. Докажите, что можно выбрать некоторую точку
вращается по часовой стрелке вокруг центра P до тех пор, пока она впервые не пройдет через другую точку множества S. В этот момент эта точка, обозначим ее Q, становится новым центром, и прямая продолжает вращаться по часовой стрелке вокруг точки Q до тех пор, пока она снова не пройдет через точку множества S. Этот процесс продолжается бесконечно. Докажите, что можно выбрать некоторую точку 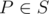 и некоторую прямую
и некоторую прямую 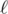 , проходящую через P, так, что для мельницы, начинающейся с
, проходящую через P, так, что для мельницы, начинающейся с 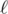 , каждая точка множества выступит в роли центра бесконечное число раз.
, каждая точка множества выступит в роли центра бесконечное число раз. - Пусть
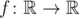 - функция, определенная на множестве действительных чисел и принимающая действительные значения, такая, что f(x + y) ≤ yf(x) + f(f(x)) для всех действительных x и y. Докажите, что f(x) = 0 для всех x ≤ 0.
- функция, определенная на множестве действительных чисел и принимающая действительные значения, такая, что f(x + y) ≤ yf(x) + f(f(x)) для всех действительных x и y. Докажите, что f(x) = 0 для всех x ≤ 0. - Дано целое число n > 0. Имеются чашечные весы и n гирь, веса которых равны 20, 21, ..., 2n - 1. Все n гирь выкладываются одна за другой на чаши весов, то есть на каждом из n шагов выбирается гиря, которая еще не выложена на весы, и добавляется либо на левую, либо на правую чашу весов; при этом гири выкладываются так, чтобы ни в какой момент правая чаша не была тяжелее левой. Найдите количество способов выполнить такую последовательность шагов.
- Пусть f - функция, определенная на множестве целых чисел, принимающая целые положительные значения. Известно, что для любых целых чисел m и n разность f(m) - f(n) делится на f(m - n). Докажите, что для любых m и n таких что f(m) ≤ f(n), число f(n) делится на f(m).
- Пусть ABC - остроугольный треугольник, и Γ - описанная около него окружность. Пусть прямая
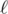 - некоторая касательная к окружности Γ, и пусть
- некоторая касательная к окружности Γ, и пусть 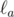 ,
, 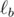 и
и 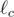 - прямые, симметричные прямой
- прямые, симметричные прямой 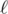 относительно прямых BC, CA и AB соответственно. Докажите, что окружность, описанная около треугольника, образованного прямыми
относительно прямых BC, CA и AB соответственно. Докажите, что окружность, описанная около треугольника, образованного прямыми 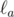 ,
, 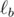 и
и 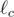 , касается окружности Γ.
, касается окружности Γ.











Так?
Что-то слишком просто.
Действительно, возьмем два минимальных простых делителя n: p < q. Рассмотрим разложение ap + bq = 1. Ясно, что f(ap) - 1 = p - 1, а f(bq) = q. Но p - 1 на q не делится. Противоречие.
Тогда f(m+n) - число большее f(n) и f(m), не делящееся на них. То есть, продолжая, можно построить неограниченную возрастающую последовательность значений функции. Но они ограничены сверху f(0). Противоречие.
(Все равно слишком просто, наверно, опять где-то баг.
Решение ниже мне больше нравится, там, кажется, и ошибиться негде).
Если f(n) и f(m) взаимно просты, то такое число единственно по модулю произведения (и мы его знаем). Если не взаимно просты - то тоже, надеюсь, единственно по по модулю НОК. Нет?
А почему все делятся на f (1)? Для отрицательной полуоси как-то неочевидно (зато там все делится на f (-1)).
upd. Потому что предыдущий комментарий, например.
Пусть m>n и f(m)!=f(n). Рассмотрим тройку чисел m, n и m-n. f(m) - f(n) делится на f(m-n), f(m) - f(m-n) делится на f(n) и f(n) - f(m-n) = f(n) - f(n-m) делится на f(m). То есть среди чисел f(m), f(n), f(m-n) разность любых двух делится на третье и не все три числа равны. Выберем 2 меньших из трех, их разность делится на число большее их обоих, значит их разность 0. То есть 2 числа равны. Из предположения следует, что одно из этих чисел f(m-n). Пусть f(m-n) = f(n), тогда f (m) - f(m-n) делится на f(n), то есть f(m) - f(n) делится на f(n), значит f(m) делится на f(n), аналогично если f(m-n) = f(m).
Решение первой задачи.
Кстати, а почему в правках latex не показывается?
Хотя... наверное это решение все же точно такое же как предыдущее.
Спасибо, кэп =)
P.S. Спасибо всем, я наконец-то понял =)
Пока результатов нет а он сам уже на IOI
Вроде бы 3+.
Про остальных:
Крачун, Пахарев, Григорьев - 4
Бурова, Циглер - 3.
медалей .
А то из 7 баллов можно заработать только 1 при правильном ответе и случайно пропущенном переходе, который как Вам кажется очевиден и неважен.
Если что, я про теорему Тарского.
P.S. написал сообщение под этим аккаунтом чисто из-за просьбы на аватарке, не хочу иметь много аккаунтов :)
http://official.imo2011.nl/participant_r.aspx?id=8473
Так что rng_58 — босс.
P. S. Ни за что бы не узнал про rng, если бы не замечание Александра + его имя не было бы раскрыто в поздравлении победителей финала Яндекса.
Как-то очень фраза не понравилась. Уничижительно по отношению к СП. А может все наоборот? Paul Jefferys, rng за счет знания математики чего-то достигли в СП. К чему всегда и стремились.
Во-первых, олимпиадная математика в некотором смысле хобби, равно как и СП, поэтому "развлекаться", даже лучше "увлекаться" — эти слова сопутствуют обоим видам деятельности.
Кроме того, я отдельно упомянул тех людей, чьи результаты на главной школьной мат. олимпиаде в некотором смысле выдающиеся (за всю историю ее существования, а это полвека). Показалось интересным то, что многие их них увлекались и СП.
Далее, я не совсем понял (видимо, Вы увидели в моих словах больше, чем нужно), что именно наоборот?
Если Вы про то, в каком порядке они занимались тем и другим, то сами же называете последовательность.
Действительно, учитывая то, что СП продолжается (если не с большей силой) в студенческие годы, а также то, что приложить навыки решения мат. олимпиадных задач к СП кажется более выполнимой задачей, нежели наоборот, то скорее всего, порядок именно таков.
Кроме того, не стоит за людей решать, к чему и где они стремились. И уж точно абсурдно предположение о том, что человек, четыре раза ездивший на IMO, делал это ради СП (равно как и если бы это происходило с точностью до наоборот).
Вопрос к математикам: а можно ли подобные книги найти на русском языке?
Нас обошли Китай, США (в составе которых на этот раз четыре китайца) и... встречайте, великолепный Сингапур!
А еще кое-кто поставил новый рекорд — теперь лидируют два немца.
Правильно ли я понял из википедии, что в Германии школу заканчивают в среднем на два года позже, чем в России?
Пять с плюсом за внимательность!