Недавно в Голландии прошел subj. Результатов я пока не видел, но русские условия уже есть. Перепечатаю их сюда. Если кому-нибудь интересно, можно обсудить задачи. :)
Интересно, есть ли на codeforces участники IMO 2011? А прошлых лет?
- Для множества A = {a1, a2, a3, a4}, состоящего из четырех попарно различных целых положительных чисел, обозначим через sA сумму a1 + a2 + a3 + a4. Через nA обозначим количество пар индексов (i, j), 1 ≤ i < j ≤ 4, для которых sA делится на ai + aj. Найдите все множества A, состоящие из четырех попарно различных целых положительных, для которых nA принимает наибольшее возможное значение.
- Пусть S - конечное множество точек на плоскости, содержащее хотя бы две точки. Известно, что никакие три точки множества S не лежат на одной прямой. Назовем мельницей следующий процесс. Вначале выбирается прямая
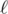, на которой лежит ровно одна точка 
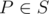. Прямая 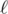вращается по часовой стрелке вокруг центра P до тех пор, пока она впервые не пройдет через другую точку множества S. В этот момент эта точка, обозначим ее Q, становится новым центром, и прямая продолжает вращаться по часовой стрелке вокруг точки Q до тех пор, пока она снова не пройдет через точку множества S. Этот процесс продолжается бесконечно. Докажите, что можно выбрать некоторую точку 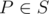и некоторую прямую 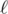, проходящую через P, так, что для мельницы, начинающейся с 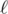, каждая точка множества выступит в роли центра бесконечное число раз. - Пусть
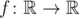- функция, определенная на множестве действительных чисел и принимающая действительные значения, такая, что f(x + y) ≤ yf(x) + f(f(x)) для всех действительных x и y. Докажите, что f(x) = 0 для всех x ≤ 0. - Дано целое число n > 0. Имеются чашечные весы и n гирь, веса которых равны 20, 21, ..., 2n - 1. Все n гирь выкладываются одна за другой на чаши весов, то есть на каждом из n шагов выбирается гиря, которая еще не выложена на весы, и добавляется либо на левую, либо на правую чашу весов; при этом гири выкладываются так, чтобы ни в какой момент правая чаша не была тяжелее левой. Найдите количество способов выполнить такую последовательность шагов.
- Пусть f - функция, определенная на множестве целых чисел, принимающая целые положительные значения. Известно, что для любых целых чисел m и n разность f(m) - f(n) делится на f(m - n). Докажите, что для любых m и n таких что f(m) ≤ f(n), число f(n) делится на f(m).
- Пусть ABC - остроугольный треугольник, и Γ - описанная около него окружность. Пусть прямая 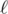- некоторая касательная к окружности Γ, и пусть
, 
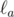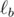и 
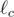- прямые, симметричные прямой 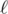относительно прямых BC, CA и AB соответственно. Докажите, что окружность, описанная около треугольника, образованного прямым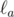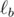и , и 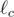, касается окружности Γ.
Comments (0)
