Пытался найти блог про гран-при, не нашел и решил создать сам. Предлагаю обсудить задачи здесь. Очень интересно решение задач B,F,G.
На счет задачи о шестеренках (N)
Представим наши шестеренки как вершины графа, проводим ребра если шестеренки касаются друг друга. Дальше запускаем бфс или дфс разницы нет. И проходим по всем шестеренкам, если в какой-то не были запускаем дфс от нее. Теперь главная проблема была в том, что радиусы могут быть до 10^4, а разница в скоростях двух смежных шестеренок пропорционально отношению их радиусов. Из-за этого по-видимому шло переполнение. Для того чтобы этого избежать я хранил отношение скоростей шестеренок, ни как одно число,а в виде массива всех простых чисел от 1 до 10^4 включительно.
Автокомментарий: текст был обновлен пользователем the_art_of_war (предыдущая версия, новая версия, сравнить).
How to solve J?
Solved by Egor Chunaev ch_egor with Simulated annealing (Global optimisation)
I don't know normal solution, but this AC.
Solution by mmaxio: Erdős-Ginzburg-Ziv theorem says that set of size 2*n-1 for sum n is enough to be sure that subset with good sum exists; therefore one of possible solutions is to compress numbers to be able to solve naive knapsack, and then decompress result to get answer in terms of original problem.
If you need to get 2016 and you have 6666 numbers — you can group all odd numbers in pairs and all even numbers in pairs (if some number don't have a pair — throw it away); now you need to get even sum, and in all pairs sum is also even, so you can divide everything by 2 and start solving problem where you need to get 1008 and there are at least 3332 numbers.
Repeat it again to get 504... 252... 126... 63 :)
Now you need to get sum divisible by 63 with a set of ~200 numbers. EGZ theorem says it is always possible, so you can solve a straightforward knapsack, get some result and decompress it (because right now every your "number" means 32 numbers of original array).
Or we can do bruteforce and solve for 3 (twice) and for 7.
Explanation in Russian. For primes (2, 3, 7) you can just enumerate all possible subsequences or solve via knapsack.
Интересно, как решается задача о шестеренках div 2. Очень интересует 6 тест. Спасибо.
Проверяем двудольность и достижимость последней вершины bfs'ом. Если всё ok, ответом будет отношение последнего радиуса к первому. Знак определяется долей, а которую попала последняя вершина.
Я как бы так и делал, но что-то не пошло. А можно Ваш код глянуть. Спасибо.
http://pastebin.com/4VLsVzCz
F: Заметим, что массив A — это такая перестановка, в которой или все эелементы после i-го строго больше чем i-ый, или строго меньше чем і-ый для любого i.
Видем несложную динамику — стоим в массиве a на позиции p1, в массиве b — на позиции p2, наш текущий минимум равен min1, максимум — max1. Динамика говорит, можем ли построить ответ при таких параметрах Сложность выходит большая — O(n*m^3). Оптимизим следующим образом: убираем из состояния max1, и теперь наша динамика не говорит yes/no, а пробует максимизировать max1. Таким образом у нас теперь сложность O(n*m^2).
Код
Автокомментарий: текст был обновлен пользователем the_art_of_war (предыдущая версия, новая версия, сравнить).
B: Давайте разделим на две доли, возьмем меньшую долю и переберем битмасками все возможные ее состояния. Теперь нужно для заданной битмаски с левой доли посчитать количество способов обработать вторую долю. Давай назовем вершину, что входит в D хорошей. Назовем плохую вершину, у которой есть соседняя хорошая — покрытой. Тогда все соседние вершины правой доли для хороших вершин из левой доли могут быть плохими (назовем, потенциально плохие). Всего вариантов их обработать 2^количество. Но некоторые из таких обработок не покрывают плохие вершины из левой доли. Эти варианты можно учесть через включения-исключения по всем подмаскам маски текущих плохих вершин левой доли. Мы предполагаем, что текущая подмаска полностью не покрытая, и вычитаем из маски потенциально плохих все соседние текущей подмаски. Итого
http://ideone.com/0YU0fL
Автокомментарий: текст был обновлен пользователем the_art_of_war (предыдущая версия, новая версия, сравнить).
A зачем запускать dfs из каждой непосещенной вершины, если мы запустили его с 1 и не нашли пути в последнюю, то ответ -1. Разве не так?
да не нужно, запускаем дфс всего один раз. Я имел в виду запускаем для непосещенной вершины внутри дфс.
Понятно. Спасибо.
Автокомментарий: текст был обновлен пользователем the_art_of_war (предыдущая версия, новая версия, сравнить).
B:
Разобьем граф на компоненты связсности. Найдем ответ для каждой компоненты, перемножим их.
Теперь как решать для компоненты. Разобьем ее на две доли. Переберем подмножество меньшей доли, которое вошло в ответ. Найдем все вершины большей доли, которые сейчас не соединены ни с чем — они точно войдут в наше текущее множество выбранных вершин, обновим на их основании множесто вершин меньшей доли, для которых уже все ОК (для вершины все ОК либо если она входит в множество, либо ее сосед входит в множество). Остальные вершины большей доли мы можем как брать, так и не брать — единственное ограничение: в конце все должно быть ОК для всех вершин меньшей доли. Пишем динамику по номеру вершины большей доли и подмножеству вершин меньшей доли, для которых все ОК. Динамика считает сколько осталось способов выбрать вершины большей доли, чтобы описанное выше условие выполнилось. Переход — берем или не берем текущую вершину.
О сложности. Заметим, что то что мы написали (с кучей запусков динамики), равносильно другой динамике — в ней маска троичная (вершина или входит в выбранное множество, или уже покрыта соседом из большего множества, либо вообще не покрыта), а все остальное такое же. В ней состояний очевидно O(3n / 2 * n).
Код: http://pastebin.com/XDFWL13x
UPD Опередили
G: Давайте посчитаем сумму результатов, а потом поделим на количество различных течений игры. Обозначим числа из нашего массива за x1, ..., xn. Тогда легко понять, что ответ является симметрическим многочленом от x1, ..., xn без свободного коэффициента, то есть представляется как сумма элементарных симметрических с какими-то коэффициентами (полезно, что
— поле, хотя потом окажется, что все коэффициенты целые).
Пусть теперь мы каким-то образом узнали значения коэффициентов перед симметрическими многочленами. Узнать значения симметрических многочленов от каких-то конкретных значений a1, ..., an — это в точности коэффициенты многочлена (x + a1)(x + a2)... (x + an). За квадрат мы как нибудь их перемножим.
Теперь нам осталось только узнать коэффициенты перед симметрическими многочленами, или (так проще, как мне кажется, думать) коэффициенты перед одночленами x1x2... xk. Обозначим за d(n, k) коэффициент перед одночленом x1x2... xk, если изначально было n переменных x1, ..., xn.
Давайте выразим d(n, k) через d(n - 1, k) и d(n - 1, k - 1). Пусть на первом шаге мы соединили xl и xr, l < r. Пусть сперва мы сделали операцию сложения. Есть следующие варианты, как мог образоваться одночлен x1x2... xk:
Тогда при фиксированных l, r легко однозначно определить одночлен степени k, из которого он пришёл. Такое могло произойти k(n - k) способами. Пусть теперь мы сделали операцию умножения (нумерация случаев аналогична):
Итого,
. Такая динамика легко считается за квадрат, что вкупе с уже сказанным даёт нам решение за O(n2).
Код.
How to solve C? It looks difficult even when Q = 1.
Kuhn solutions was passed.
And repeat it Q times independently?
No. Once you have initial solution it is easy to update it with O(1) dfses for each query.
Gassa has test on which author's (and all the participants from Petrozavodsk training camp) solution gets TLE.
As you mention it, I'll describe the test here. It's rather simple: a chain of length Θ (n) which must be traversed by too many augmenting paths if we order the vertices according to their weight, leading to Θ (n2) performance.
Picture for n = 10 and w = 1..5:
The actual test has n = 200000 and w = 1..10000. Generator (Python 2 & 3): http://pastebin.com/KFTvgDXG.
Now, perhaps this particular test can not trick every possible Kuhn solution. However, as this test already posed a problem to every solution we had near the end of the contest, including the authors' solution, we didn't try to craft a better one.
This paper describes the solution for Q = 0 (with
(complexity of max matching), using tricky divide-and-conquer approach). For queries, it seems that it is enough just to run single DFS from a changed vertex. I wonder if someone managed to implement the proper solution during the contest...
How to solve H? I can't solve it better O(N^3)
The following passed in upsolving (idea by meshanya, he probably knows how to prove, I didn't entirely understand his proof during the contest).
Suppose the tree is a chain. Then you can easily solve it in n2 with a standard idea (Knuth optimization). The idea is that when computing answer for a segment l, r, point of optimum is between points of optimum for l, r - 1 and l + 1, r. This still holds for tree, but the restriction doesn't give us quadratic time. To make it quadratic, one needs the following observation: suppose there's a node v with kids w1 and w2 with corresponding costs c1, c2, and c1 ≤ c2. Then for every segment (u, w2), point of optimum has an upper bound of point of optimum for (u, w1) (simply speaking — if we increase the last number, point of optimum cannot move to the left). This adds another restriction to restrictions from Knuth optimization, and makes running time quadratic (I don't entirely understand why).
A long line of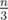
ones that breaks up in 
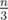paths of length two with numbers 1, 109 (in that order) should break this, shouldn't it? You will run O(n) iterations of search for optimum point for all O(n2) paths that end in leaves anyway (because optimum point for all paths except paths to leaves is somewhere around middle of the long line).
Something like this:
Hm, on this test, the solution indeed seems to work longer than n2 :) So we can say it is well-deserved that we didn't get it during the contest. Though runtime is only ~3 seconds for the test, so even if it is cubic, it seems to be rather fast.
How about slight improvement — first element of long path is 109 instead of 1? It should be even worse.
UPD. Sorry for spamming, but it seems that I understood why it is not much worse and 106 as first element instead of 109 should work.
Not much worse — around 3.2 seconds. Though this is my local workstation, I tried on Yandex.Contest servers, and it successfully times out.
Could you show me ur code for this problem? I added ur last optimization, and it gets wa31 :(
Sure, here it is. Keep in mind that it is actually n3, as discussed above.
Try to solve the problem on array using Convex-Hull-Trick instead of Knuth optimization (store some functions in stack, each pair of those functions should have no more than one intersection). This approach can be done on tree if we will store all the values accurately.
На каком сайте можно порешать эти задачи?
вот
А это вообще считается нормой, что в одном этапе открытого кубка аж по трем задачам у большинства участников проходили неправильные решения (я говорю про задачи C, H, J): одной из самых популярных задач была J, в которой большинство команд сдавали рандом (Burunduk1 на разборе сказал, что умеет ломать все рандомшафлы и сортировки) и пихали битсеты с огромной асимптотикой; задача H в которой в зависимости от нахаченности твоего куба (а точнее от того был ли тест против твоего куба, в частности на разборе Um_nik взломал разбираемое решение) он либо проходил либо нет (наш куб не прошёл); задача C в которой все сдавали Куна на графе из 2·105 (вон в комментах пишут, что против этого Куна у Gassa есть тест). Кстати не считая двух простых задач и задачи G это были самые популярные задачи.
Не повод ли это сделать этап анрейт? Или анрейт этапов не бывает (я просто не в курсе)?
P.S.: Да и забыл, почему мне это не очень нравится: это один из этапов Yandex.Opencup Part 3.
По B заходил (правда в дорешку уже) перебор в лоб (ребра хранить в масках). Как минимум в тестах не было даже пустых графов из большого числа вершин.
А по поводу рандомов в J предлагаю кроме обычных шафлов (в том числе с учетом элементов веса 2016) дополнительно такой:
Менять местами случайно элементы из первых 2016 индексов с остальными так, чтобы сумма в левой части уменьшалась (увеличивалась). Не смог подобрать тестов, которые завалили бы такое решение (или плохо пытался). Буду рад, если кто-нибудь подберет тест
Код решения, уменьшающего сумму (в идеале можно добавить и вариант увеличения)
Знаешь я общался с x командами по поводу задачи J и из них x - 1 команда рассказала свой рандом который прошёл и ещё одна сказала, что запихала битсеты (прям вообще втупую, кроме восстановления). Мы пробовали запихать пошафлить взять префикс большой длины, а на оставшихся сделать честный рюкзак, и не запихали.
Чтобы пройти тесты достаточно рандом шаффл + учет элементов веса 2016. Тесты ужасны. Неправильно, когда в силу слабых/странных тестов чьи-то неверные решения проходят, а чьи-то нет
Не факт, что тесты ужасны. Ведь для нахождения хотя бы одной группы 2016 чисел, сумма которых делится на 2016, достаточно 2·2016 - 1 = 4031 числа, а в инпуте их в 1.5 раза больше, поэтому есть вероятность, что невозможно сделать хорошие тесты против всяких рандом шафлов (поправьте, если кто-нибудь умеет в такое). Другое дело, что искусственно поднимать ограничения до красивого числа в такой задаче (которая, кстати, не блещет новизной), давая риск пройти всякому говну —
полный идиотизмдовольно странная затея.UPD Сорри, не заметил что Edvard написал, что Burunduk1 умеет всё это дело ломать. Кстати, интересно было бы услышать как это делать)
Против обычного рандом шаффла (учитывающего еще числа 2016, чего хватает для AC) подойдет тест состоящий наполовину из чисел 2014 и 2015, например.
Ё-мое, еще и совершенно тупой рандом шаффл заходил, я думал под этим что-то более хитрое подразумевалось. Жесть
Справедливости ради: тест против Кнута по H придумал Merkurev, я лишь озвучил :)
Сделано в Китае!
Надо признать, что тесты на финалах тоже особо не отличаются качеством. Во всяком случае, до 14 года включительно. Возможно в 15 году вместе со средней сложностью задачи поменялось и это тоже.
Более того, я взял прошедшее на контесте решение Н команды Zhukov Team (они утверждали, что оно квадратичное :) ), и на довольно тупом макстесте оно работает 8,8с (потому что на самом деле оно работает на нем за куб). Так что не только ограничения выставлены плохо в этой задаче, но и тесты действительно слабые.
И кстати я совсем забыл: этот этап является ещё и отборочным на чемпионат Татарстана. Так что совсем бред какой-то.
Да, не тот китайский контест назвали опенкапом. В птз был один хороший, один нормальный, и один стремный китайский контест. Но, как говорится, кто же знал.
После прочтения вполне обоснованного негодования стало интересно: а кто проверяет задачи Open Cup? Там же наверняка есть человек который проверяет задачи на баян/не бабаян, решаемость и т.п.
Opencup — это сборник произвольных контестов. Надежда только на авторов.
2016 * 2016 * (2016 * 2 - 1) / 64 = 255, 984, 624
А что не так с битсетами?
Про задачу H:
Если отбросить тот факт, что задача говно, на контесте уже на первом часе было понятно, что все пихают куб и надо куб этот запихнуть.
Как запихнуть куб без кучи бревен и без бубнов: http://pastebin.com/6CLufH0T
Я правда не понимаю, почему до сих пор все не прочитают статью про SSE за полчаса и не упростят себе жизнь, потому что из того что слышал я, все пихали какое-то редчайшее говно с бубнами, брейками и прочей магией.
В зависимости от того хотели ли авторы чтобы задачу сдавали так или нет.
что такое SSE ?
Во-первых, ты уже с хаками рассказываешь решение (там всё-таки чисел было 6666). Во-вторых, вроде как это ещё восстанавливать надо (тоже хаками решается). В-третьих я думаю, что ограничения выставлены неудачно (решение с битсетами наверняка не предполагалось проходящим).
Про SSE наверное ты прав. Я несколько раз читал решения участников на CF с SSE, но если честно плохо разобрался (видимо надо прочитать нужную статью, только по коду не очень понятно).
I've found a paper with an algo which could be used to solve problem H in O(n2). Here it is. Though I didn't yet manage to read it at large.
The problem with Knuth optimization is that its time bound is amortized: although it runs in quadratic time we cannot just add one element to the array in worst-case O(n), counter-tests could be found above. However, there is a method similar to Knuth optimization with same time complexity but worst-case. It allows adding elements to the back of the array. It is described in the paper. Given this, problem H is trivial: just traverse the tree, adding elements and rolling back on the way.
I think last weeks Opencup problems were added in the gym. Would have been awesome if this was added in the gym too.