Swistakk's blog

Random Walk: Hard version
By Swistakk, history, 9 years ago, In English

Hi!
On recent OpenCup — Makoto Soejima Contest 4, problem "Random Walk" was posed. We were requested to determine the expected number of visited cells after n steps of random walk on a plane — in each move from (i, j) we go either to (i+1, j), (i-1, j), (i, j+1) or (i, j-1) — all with prob 1/4. More precisely, we needed to output 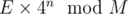, where M was some integer. In this problem constraint was n ≤ 5000. Actually, this problem becomes much more interesting if we try to solve it for n ≤ 105 in a reasonable time (assume M = 109 + 7 for simplicity). Can you see the solution (if I'm not mistaken — it exists)?

  • Vote: I like it
  • +80
  • Vote: I do not like it

»
9 years ago, # |
← Rev. 4   Vote: I like it +18 Vote: I do not like it

I have a solution with complexity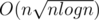 . We have the following O(n2) solution:

,

,

.

Let's calculate zk using sqrt-decomposition, so

, where b is the position of the start of block. The first sum we can calculate for all k after each block using FFT. So we have complexity from the above .

Working time for n = 105 is 14.12s, but it's not optimized, so it can be decreased a lot. Code.

UPD: Actually it works in time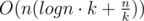 , so for 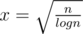we have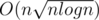

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    It seems that I understand how to speed up your solution to . Basically, we have two arrays. One is known beforehand (wi), elements of other are revealed to us one by one (zi) and we want to find their convolution. Solution to this problem can be seen here (check editorial of problem Div 1 E).

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Yes, that's the approach I had in my mind :). If put in other words, problem we are dealing with is finding an inverse (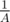) of a generating function and such approach leads to complexity, whereas straightforward computations of course give O(n2).

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +20 Vote: I do not like it

      Actually today I was solving CF309 in a virtual mode and right before I seen this blog entry I was trying to solve the problem E using the same technique as here 16036613 (without editorial) and it got TL. It seems I should look at the editorial the improve my solutions for both problems :-)

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Got it. Very nice idea. Both my solutions with sqrt-decomposition and that idea gives the answer modulo 109 + 7 352371679 for n = 105. The second one works in time 7s.

      → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    Glad that you gave this probem a shot and indeed that's a good direction, however there are still some issues. First of all w2k should be equal to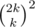 , but you got it right in your code :). If length of block was taken with more care, I think we can achieve 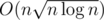using the same approach, however my solution runs in .

    For those, who are not familiar with basic version of this problem, wk was meant to be number of paths of length k which end up in their start position and zk is number of paths of length k that do not ever visit their start position again. Presented formula for wk is really nice, but also hard to derive, observing it is a significant part of improving running time (for n ≤ 5000 it can be simply bruteforced by fixing number of horizontal moves), I encourage readers not familiar with this to think a while about it :).

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      If I'm not mistaken, we need to calculate this sum: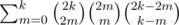

      After reducing some factorials we have:

      For calculating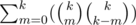 we can say, that it's coefficient of the monomial xmyk - mxk - myk = xkyk in (x + y)k(x + y)k, which is obviously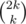

      Am I right?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Nice, I didn't know that this can be so simply done by calculating factorials, that's correct :). Btw the last argument can be replaced by using very easy Vandermonde's indentity https://en.wikipedia.org/wiki/Vandermonde%27s_identity

        However there is still a way to prove this without any calculations, hint: it makes coordinates "independent"

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          I wrote below the simple proof.

          → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks. I fixed the formula. I was in a hurry so I didn't have time to find the optimal size for the block. Now I updated it.

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it +10 Vote: I do not like it

      It's easy to prove the formula for wk: we can assign the signs (plus/minus) to the directions in a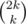 ways and also we can assign the axis (x or y) to the directions in a 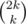ways, so we have .

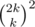      UPD: There is a mistake in proof see the comment below.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it +8 Vote: I do not like it

        That's a bit more complicated. Before that, we need to rotate whole coordinate system by 45 degrees and instead of considering coordinates (x, y) we need to look at (x + y, x - y), which I consider really tricky and insightful. Before rotating changes are of type ( + , 0), ( - , 0), (0,  + ), (0,  - ) and after rotating they are exactly what you wanted to ( + ,  + ), ( + ,  - ), ( - ,  + ), ( - ,  - ) (which was basically whole difficulty in problem C5 on Petrozavodsk, which was solved just by 6 teams).

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Of course you are right, I hurried one more time). On one of the problem analysis in Petrozavodsk this winter aid uses the same trick with rotating of coordinate system.

          → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Btw, I learned that rotating trick from this problem: http://codeforces.net/contest/538/problem/G

        → Reply