Блэкджек (задача A, 2-ой дивизион). Автор задачи - Alex_KPR | ||
| Очевидно, что масти никакой роли не играют. Рассмотрим теперь подробно все случаи: [0 - 10] — ноль способов. | |
| Сложность алгоритма — O(1). |
| Проверка штанов на унылость (задача B, 2-ой дивизион; задача A, 1-ый дивизион). Автор задачи - Alex_KPR | |
| Заметим, что мы не можем добраться до i + 1-го вопроса до тех пор, пока не кликнем на все ответы на i-м вопросе. Из всех ответов на i-ом вопросе нас вернут в начало ai - 1, и только один отправит дальше. Каждый неверный ответ заставит проделать нас путь длины i - 1 плюс единицу за клик по неверному ответу. Отсюда формула для перехода на i + 1-ый шаг: ci = (ai - 1)· i + 1 (нумерация с единицы). Просуммируем все значения ci для получения ответа на задачу. | |
| Сложность алгоритма — O(n). |
| Ктулху (задача C, 2-ой дивизион; задача B, 1-ый дивизион). Автор задачи - Alex_KPR | |
| Внимательно прочитаем формальную часть условия. Ктулху должен представлять собой простой цикл длины три и более, каждая вершина которого является корнем дерева. Заметим два важных факта: а) Ктулху — это связный граф Если к дереву из трёх и более вершин добавить ровно одно любое ребро (не мультиребро и не петлю), то мы получим граф, обладающий свойствами а) и б). Отсюда простое решение: проверим граф на связность (это можно сделать одним поиском в глубину) и проверим условие n = m. При выполнении обоих условий граф является Ктулху. | |
Сложность алгоритма — O(m). |
| Русская рулетка (задача D, 2-ой дивизион; задача C, 1-ый дивизион). Автор задачи - Alex_KPR | |
| Разберёмся с задачей сперва в случае чётного n. Очевидно, что при k = 1 ставить патрон нужно в крайнюю правую позицию, то есть, например, при n = 8 ответ будет выглядеть так: .......X Оценим вероятность застрелиться в этой ситуации. Напишем нули у тех слотов барабана, которые приведут нас к поражению, а у победных напишем единицы: 10101010 Отсюда понятно, что каждый следующий патрон нужно ставить так, чтобы не снижать вероятность собственной победы до тех пор, пока это возможно. Когда все слоты, ведущие к поражению, будут заполнены патронами, останется только получать лексикографически наименьший ответ с ростом k. Рассмотрим ответы для всех остальных k при n = 8: .....X.X В случае нечётного n рассуждения будут немного иными в начале, давайте построим ответ для n = 9 и k = 1: ........X Можно поставить патрон аналогично чётному случаю, как описано выше. А можно поступить иначе — зарядить первый слот и сдвинуть барабан влево, смотрим: X.......X => .......XX Очевидно, что вероятность не изменилась, а ответ улучшился. Дальше придётся заряжать револьвер так, как описано для чётного случая: .....X.XX Разобравшись в принципе заполнения барабана патронами не должно составить труда научиться с помощью нескольких условий быстро отвечать на требуемые запросы. | |
Сложность алгоритма — O(p). |
| Время грабить корованы (задача E, 2-ой дивизион; задача D, 1-ый дивизион). Автор задачи - Alex_KPR | |
| Будем решать задачу оффлайн. Считаем все запросы и отсортируем их по возрастанию параметра b. После этой операции существует несколько эффективных решений, рассмотрим, как мне кажется, наиболее идеологически простое из них. Для этого изучим два следующих алгоритма: 1. Для каждого (a, b)-запроса пробежим по массиву и вычислим результат тупо в лоб, то есть: for(int i = a; i < n; i += b) 2. Для фиксированного b посчитаем за линию динамику, чтобы научиться отвечать на запросы для произвольного a за O(1): for(int i = n - 1; i >= 0; i--) Очевидно, что 1-ый алгоритм будет неэффективен при малых значениях b, а 2-ой — при очень разных b. Заметим, что не бывает такого теста, при котором все b достаточно малы и притом различны. Отсюда простая идея: будем решать задачу 1-ым алгоритмом при больших значениях b (больше некоторого c) и 2-ым при малых (меньше и равном c). Сортировка вначале нужна для того, чтобы не пересчитывать динамику для фиксированного b. Можно доказать, что при выборе c равном |
|
Сложность алгоритма — |
| Закупка множеств (задача E, 1-ой дивизион). Автор задачи - winger | |
| Разбор задачи провёл winger. Построим двудольный граф G1 с множествами в левой доле и числами в правой доле. Ребро из множества в число проведем, если число принадлежит множеству. По теореме Холла, из условия "известно, что объединение любых k множеств содержит не менее k различных чисел (для любого целого положительного k)" и из того, что различных чисел не больше n, вытекает существование полного паросочетания, (включающего все вершины). Найдем в G1 какое-нибудь такое паросочетание M = {(ui, vi)}. Теперь построим ориентированный граф G2 с вершинами, соответствующими множествам и ребрами (ui → uj) для всех ребер (ui, vj) в G1 не из M. Любой искомый набор множеств размера k не должен содержать в G2 ребер из набора наружу (иначе в нем будет находиться k чисел из паросочетания + количество вершин не из набора в которые есть ребра из набора). Таким образом, задача свелась к следующей: в ориентировам графе с весами на вершинах найти набор вершин минимального суммарного веса без ребер наружу. Эта задача, как известно, сводится к задаче поиска минимального разреза. Напишем на ребрах G2 бесконечные веса, добавим вершины s и t, и для каждого множества ui с весом w нарисуем ребро ui → t с весом w если w > 0 или ребро s → ui с весом - w если w < 0. Доля, содержащая s в минимальном разрезе получившегося графа из s в t, будет соответствовать искомому оптимальному набору. |
|
Асимптотическая сложность решения — O(n3). |



 будет достигнута оценка
будет достигнута оценка 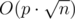 .
.







Can anyone explain why the complexity for Time to Raid Cowavans (Div1-D) is O(P * sqrt(N))? I'm new to this complexity analysis stuff
Because we use 1-st method only for queries where
B >= sqrt(N), so each query runs inO(sqrt(N))time. 2-nd method worksO(n)time for initializing arrayd, andO(1)to answer each query. We don't need more thansqrt(N)initializations, because we use 2-nd method only for groups of queries whereB < sqrt(N). Total complexity isO(sqrt(N) * p1 + sqrt(N) * N + p2) = O(sqrt(N) * max(N, P)).p1— number of queries whereB >= sqrt(N), andp2 == p - p1.Thanks for the detailed explanation!
Exactly, so there is a mistake in the solution where they say the complexity is O(sqrt(n) * p). It's actually O(sqrt(n) * max(n, p).
Может ли кто-нибудь пояснить, почему вторая часть задачи E эквивалентна нахождению минимального разреза?