A. (ссылка) В этой задаче нужно было сделать то, что было написано в условии. А именно: считать все имеющиеся навыки, затем степень их владения домножить на коэффициент k, после этого выкинуть все навыки, степень владения которых меньше 100. Далее нужно было добавить новые навыки (то только те, которых еще нет в списке). Полученный список отсортировать и вывести.
***
Проблема с точностью при умножении вещественных чисел для автора стала неожиданной. То есть на самом деле такой ловушки не планировалось. Авторское и проверочные решения сразу считали все в целых числах, а мысль о возможных проблемах даже не возникла. Впрочем, это еще раз подтверждает следующее правило в олимпиадном программировании: очень внимательно относиться к сравнениям вещественных чисел, а по возможности все делать в целых числах.
B. (ссылка) Решение сводится к перебору всех возможных распределений конфет, подсчету вероятности утверждения решения в каждом из случаев с выбором максимума.
Общее количество распределений Ck + n - 1n - 1, что в худшем случае не превосходит 6435. Зафиксируем распределение и вычислим величины zi = min(li + ci × 0.1, 1.0), где zi - вероятность того, что i-ый сенатор проголосует за, li - лояльность сенатора, ci - количество конфет, которые мы отдаем i-му сенатору.
Подсчет вероятности можно делать за время O(2nn), а именно: переберем все маски длины n. 1 будет означать, что соответствующий сенатор проголосовал за, 0 - против. Вероятность получения такой маски равна mmask = П(zi × [i - йсенаторпроголосовалза] + (1 - zi) × [i - йсенаторпроголосовалпротив]), где [true] = 1, a [false] = 0. Теперь для каждой маски найдем вероятность того, что предложение будет утверждено. Оно равно smask = 1 если голосов за больше половины и smask = A / (A + B) в противном случае, где B - сумма уровней сенаторов, что проголосовали против. Таким образом, вероятность для зафиксированного распределения конфет равна 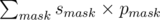 .
.
Решение имеет сложность O(Ck + n - 1n - 12nn).
***
На самом деле изначально эта задача была несколько сложнее (эдак уровня D). Но затем было принято решение ее сильно упростить))
C. (ссылка) В этой задаче нужно было заметить, что если хотя бы в одном предмете занято не все место, то резидентов можно переместить абсолютно любым образом. Это утверждение несложно доказать. Иначе резидентов перемещать вообще нельзя.
Еще одна вещь, которую можно было заметить: в оптимальной экипировке все предметы имеют максимально возможные нужные параметры, то есть совершенно не важен порядок выбора самых крутых предметов. Более того, предметы разных классов и резиденты разных типов друг на друга не влияют. Поэтому изначально все предметы и всех резидентов можно разбить на группы по классам и по типам, а затем три раза решать одну и ту же задачу для групп (оружие, гладиаторы), (броня, охранники), (сферы, целители).
Итак задача имеет 2 случая: резидентов перемещать нельзя и резидентов перемещать можно.
1. Для каждого предмета найдем его характеристики с учетом всех резидентов, что в нем находятся. После этого выберем тот предмет, где характеристика максимальна.
2. Отсортируем всех резидентов по убыванию бонуса. После этого переберем все предметы и попробуем поместить туда максимум самых сильных резидентов и посчитаем значение параметра, которое при этом получается. Теперь просто выберем предмет с максимумом параметра.
Во втором случае есть небольшая ловушка: в трех выбранных предметах может оказаться слишком много свободных мест - больше, чем их было до перемещения резидентов. Такая ситуация невозможна, поскольку выкидывать резидентов из предметов мы не можем. Поэтому перед выводом ответа можно было просто жадно заполнить пустые места неиспользованными резидентами.
***
Изначально первый случай задумывался как ловушка и его планировалось поместить в претесты. Но затем, исходя из общей сложности контеста, было решено переместить его в примеры.
D. (ссылка) Эта задача решается с помощью структуры данных система непересекающихся множеств (disjoint set union или dsu) с эвристикой сжатия путей.
В качестве вершин dsu выступают группы одноцветных гео-панелей. Вся важная информация о группе хранится в представителе группы, а именно: размер группы (количество гео-панелей в ней), ее цвет, а так же список гео-символов, что сейчас находятся в этой группе, по еще не уничтожены. Изначально все вершины - это отдельные гео-панели, которые сразу же при генерации нужно объединить в группы по цвету.
Также заведем очередь (та самая, что описана в условии задачи), в которой будем хранить гео-символы, а именно: их цвет и место на карте, откуда они были перемещены при уничтожении.
Также нам понадобится ассоциативный массив (вроде std::map в с++), который по цвету возвращает группу из dsu этого цвета.
Еще дополнительно заведем массив размера 2n × 2m, в который сохраним спираль. Ее мы будем использовать для сортировки гео-символов.
Предложенная система структур данных позволяет проэмулировать весь процесс достаточно быстро.
Итак, поместим в очередь начальную пирамидку гео-символа, а также сгенерируем спираль и начальные состояния dsu и ассоциативного массива.
После этого делаем следующее, пока очередь не опустеет:
Извлекаем гео-символ из очереди и нарекаем его текущим. По его координатам на карте через dsu находим группу, в которой он находится и узнаем цвет группы. Далее проверяем цвета группы и гео-символа и определяем нужно ли перекрашивать данную группу.
Если ее надо перекрасить, то прибавляем ее размер к ответу. Далее сортируем все гео-символы, что находятся в группе по числам в спирали, центр которой находится там, где располагался текущий гео-символ. В этом порядке добавляем их в конец очереди, а список в группе очищаем. После этого перекрашиваем группу с обновлением ассоциативного массива.
Может оказаться так, что у нас теперь 2 группы одного цвета (это можно узнать из ассоциативного массива). Их нужно объединить а одну - родителем только что перекрашенной группы назначаем вторую группу того же цвета и увеличиваем размер родителя.
Нетрудно понять, что предложенный алгоритм имеет сложность O(nmlognm).
E. (ссылка) Сначала оценим максимальных ответ, что мы можем получить. Он равен 42. Его можно получить из довольно очевидного максимального теста
8 10 10
9 10 10
10 10 10
Общее количество состояний, в котором может находиться персонаж без учета позиции равно 8. 2 состояния ходил/не-ходил умножить на 4 состояния никого-не-держит/держит-А/держит-Б/уже-бросил.
Итого, общее возможное количество состояний равно (8 * 42)3 = 37933056. Такое количество состояний легко умещается в память.
Далее решение представляет собой запуск поиска в глубину или ширину из начального состояния.
Почему это проходит по времени? Ведь из каждого состояния может быть порядка 60 переходов.
Дело в том, что большинство состояний не будет достигнуто. Например, следующие эвристики подтверждают это:
1. Если один персонаж держит другого, то их позиции совпадают.
2. Состояния, в которых одного персонажа держат оба других некорректны.
3. В позициях с большими номерами может находиться не более двух персонажей, а в позициях с очень большими номерами - не более одного.
Кроме того, довольно много состояний, из которых мало переходов. Это те, в которых персонажи уже ходили или уже бросали кого либо.
Более точно количество переходов можно получит написав решение. Запуск на макстесте показал, что переходов всего лишь порядка 2 × 108. Таким образом, решение проходит по времени, нужно лишь аккуратно его написать.
***
Авторское решение на С++ работает около 0,3с. Также есть решения на Java, которые работают 2,8 с и 0,8 с. В первом из них на каждый переход создается новый объект, в итоге несколько раз запускается сборщик мусора, во втором эта проблема устранена. Тем не менее, чтобы решения на Java, подобные первому, проходили, TL был поднят до 3 секунд.











Например, пусть мы взяли зеленый символ с синей панели. Перекрасили все синие панельки в зеленый и поместили в очередь гео-символы с синех панелей (которые теперь уже стали зелеными). Теперь мы рассматриваем синий гео-символ: он стоит как раз на зеленой панели, которую мы только что перекрашивали.
Поэтому достаточно изначально посчитать для каждого цвета количество гео-панелей данного цвета, далее поддерживать число S - сколько панелей текущего цвета (тот, в который в последний раз перекрашивали) у нас есть. Когда происходит перекраска в новый цвет, мы прибавляем к S количество перекрашиваемых клеток. При этом количество панелей текущего цвета обнуляем. Фактически, так и будет работать решение с СНМ.
Let's call it EPS=1e-9
Just think of it like that(pls correct me if i'm wrong):
any number within EPS of a float/double number N is considered to be equal to the number(that is if number X is between N-EPS and N+EPS, then X considered equal to N)
1. For A==B use: abs(A-B)<EPS or equivalently: B-EPS<A<B+EPS
2. For A<B use: A<B-EPS
3. For A<=B use: A<B+EPS
Now for problem A, you need to check:
K*level < 100
==> K*level < 100-EPS
==> K*level +EPS < 100, so you can calculate (int) (K*level+EPS) then compare with 100 or also compare directly K*level< 100.0-EPS
so we need to check K*level<100 NOT K*level<=100
NO, you need to take care of precision in ALL cases: <,<=,==.
For A<B you need to do A<B-EPS because we are considering any number between B-EPS and B+EPS to be equal to B. it's similar for A<=B.