Только что закончился этап Открытого Кубка.
Предлагаю здесь обсудить задачи.
В частности, интересуют задачи A и B.
Предлагаю здесь обсудить задачи.
В частности, интересуют задачи A и B.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
| Название |
|---|



B:
В A ещё можно вместо разбиения на чётные и нечётные честно выкидывать каждую точку из выпуклой оболочки и смотреть, сколько получится теперь точек на участке от предыдущей до следующей. Прикол в том, что каждая исходно внутренняя точка попадёт в не более чем два таких просмотра, и поэтому весь проход получится за то же самое линейное время. Ну, и отдельно обработать точку номер один.
Кстати, а как определить, в какие просмотры попадает каждая точка?
В моей реализации все точки лежали отсортированными по углу относительно первой, а соседние в выпуклой оболочке имели ссылки друг на друга. Тогда просто, когда выкидываешь некую точку, надо заново просмотреть все, которые лежат после предшествующей ей в выпуклой оболочке и до следующей за ней.
B можно было вообще без проверок. Рассмотрим пару соседних элементов суффиксного массива. Пусть это суффиксы длины l0 и l1. Тогда посмотрим на суффиксы длины l0 - 1 и l1 - 1. Если l0 - 1 лежит в суффмассиве после l1 - 1, то первый символ l0 равен нулю, а первый символ второго - единице. Назовем такую позицию разбиением. Очевидно, что сначала в суффиксном массиве идут позиции нулей, потом - единиц. Тогда, найдем все разбиения. Если разбиение не единственно, то ответа нет. Но, если единственно, то ответ всегда есть. Вроде бы, понятно почему: нет противоречий. Строго доказательство сформулировать не могу. Те, кто еще так писал, можете объяснить?
ДП :
a[i] = min(a[i-2]*p[i], b[i-2]*p[i-1]);
p - заранее посчитанный массив простых чисел.
Ответом будет a[n].
Заранее спасибо за помощь.
Мы заранее просчитали все значения, а потом их просто выводили. Просчитывали за О(2^n), программа выполнялась где-то 10-15 минут.
solve(id,mask,double a, double b)
id - номер простого, которое мы будем сейчас размещать.
mask - какие простые попали в первую группу
1) если id==n и a<b, то мы смотрим, улучшили ли мы результат, и если да, то запоминаем новое b-a и новую маску
2) Иначе пытаемся положить простое id-тое простое в первую группу и во вторую группу.
solve(id+1,mask|(1<<id),a*p[id],b);
solve(id+1,mask,a,b*p[id]);
При переборе можно спокойно забыть о длинке. Даблов хватает. А вот ответ по маске уже придется восстанавливать ею
А больше в этой задаче для нахождения правильного набора и не надо.
А сложность всё-таки O(2n) - от углубления в рекурсию лишнего n вроде не должно появиться :)
Конечно возьмёт. Куда он денется?
Только отдаст он 177792163538134124429312, а не столько, сколько взял.
Но нам и этого хватит, чтобы максимум найти.
Про n: Ну откуда оно появляется?
=======================================
Да, в даблах.
Я, чтобы не писать длинку, вывел сами числа через звёздочки и вставил это в виндовый калькулятор.
Там (в даблах) вроде только четыре последних числа неточно считаются.
Не проще ли вместо таких извращенств написать на Java с BigInteger ? :)
============================================
Иногда, когда пишу что-то на Java с BigInteger, кажется, что вся Java - это одно большое "извращенство" :)
================
ну кто на яве, кто на питоне извращался, а кто вот так) и вообще эта задача сплошное извращение, над ней извращались кто как мог
double
А с добавлением слова inline - меньше, чем за две...
повтор
у нас перекалк работал где-то 5 минут
ми искали первое число как максимальное число не больше квадратного корня с произведения первых N простых чисел, использовали даблом для произведений, поддерживая при етом маску использованых чисел
потом просто по маске искали ответ, длинкой
Вообще-то там сумма цешек, равная примерно 2n-1.
Решение такое (рассмотрим сразу для случая n = 30).
Разбиваем на 2 части произвольным образом - например, берем первые 15 чисел в одну половину и остальные 15 в другую. Перебираем все возможные произведения в каждой половине и складываем в массив, а затем сортируем (2 * (2 ^ 15) * (1 + log(2 ^ 15)) ~= 2 ^ 20. Дальше перебираем все числа из первой половины и для каждого бин. поиском находим самое подходящее число во второй половине ((2 ^ 15) * log(2 ^ 15) ~= 2 ^ 19).
Итого решение работает 2^20 * скорость операций с BigInteger.
P. S. Не понял, как в этой задаче использовать рюкзак. Можно пояснить?
Хм. То есть, в оптимальном ответе кол-во сомножителей в обеих частях не превышает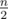 ? А почему?
? А почему?
Нужно хранить в два раза больше информации.
Рассмотрим, как считаем числа для первой половины (первые 15 штук).
Пробегаемся по всем маскам (2 ^ 15): когда зафиксировали маску, перемножаем только те простые числа, которым в маске соответствует единица. Однако еще удобно посчитать другое число - произведение тех простых, которым в маске соответствует ноль.
Таким образом, есть два массива пар бигинтов - A[2^15] и B[2^15].
Отсортировали их по неубыванию по первому числу. Понятно, что в таком случае вторые числа будут отсортированы по невозрастанию.
Пусть зафиксировали индекс i в первом массиве.
Мы хотим найти такое j во втором массиве, что
F(j) = (A[i][0] * B[j][0] - A[i][1] * B[j][1])
принимает минимальное значение. Как мы уже знаем, если j возрастает, то B[j][0] тоже возрастает, а B[j][1] наоборот убывает. А[i][0] и A[i][1] фиксированы, поэтому с возрастанием j функция F(j) также возрастает. Раз функция монотонная, применим бинпоиск. В ответ мы запишем A[i][0] * B[j][0], такое что F(i, j) минимальна (тут уже i не фиксирована). В первом множителе перемножено до n/2 простых, во втором тоже, так что количество сомножителей в ответе может превышать n/2.
Веса ребер - w[i]
Граф - неориентированный.
Ищем кратчайшее расстояние от 1 до n вершины. Если оно меньше C, то выводим Unfair и востанавливаем ответ, иначе - Fair.
Первая мысль которая возникает при прочтении задачи - макс. поток. И, вы правы, ограничения на это намекают. Немного подумав, я решил отправить в дорешивании Дейкстру не сильно надеясь на ОК. Я был очень удивлён:)
но разве там всегда выгоден поток величины 1 или просто этого условия достаточно ???!
У меня была другая проблема, не увидел в условии, что можно выбирать направление у трубы, поэтому не добавлял обратных ребер и хапнул 10 бревен. Даже писал минкост, но видимо для того чтобы убедиться в том, что поток не нужен.
Идём по действиям пользователя. В pluses[t] мы будем поддерживать количество сообщений, которые запостил пользователь:
Решение довольно простое и понятное. Я же думал над какой-нибудь крутой структурой:)
Для ясности лучше написать, что для следующего потока нужно еще один путь из 1й в Ную вершину(те ребра что уже есть ничего не дадут), который будет больше-равен 1го, то есть только ухудшит ситуацию.
Перебирай с начала без всяких отсечений.
Я написал на Java, складывал строки без всяких там стрингбилдеров, насоздавал кучу ArrayListов и все равно прога летает.
А причина в том, что таких строк всего 384 (всех возможных длин) и существуют они до длины 37.
Полконтеста пытался понять, почему моя J получает WA4 - после контеста оказалось, что в слове "defence" была опечатка :)
Как и про С и E :)
Вообще всегда считал, что в Петрозаводске не самое главное супер качество тестов, ибо все равно потом команды могут написать и правильное решение, а того лучше добавить тест против неправильного. Другое дело, что теперь эти задачи ставятся на кубок, ну и понятно, что более полный набор тестов сюда поставить нельзя ибо нельзя будет переносить результаты команд со сборов.
Я не оправдываю автора, но и наезды делать думаю, что не стоит.
E. Elections (Division 1 Only!)
Если писать динамику вперед, то получаем, что из fi, j, k можем перейти в fi + 1, j + x, k + a(i, x), где 0 ≤ x и j + x ≤ s и k + a(i, x) ≤ A с увеличение на |a(i, x) / A - vi / V| или в целых числах |a(i, x) * V - vi * A| (a(i, x) это значение ai если я выбрал из i партии x человек). Ответ для нашего A будет находится в fn, s, A.кто разобрался или решил её буду очень признателен, если сообщите (или лучше намекнете) мне в чем баг...