A. Бросок кубика
Пусть максимум из очков Якко и Вакко -- a. Тогда Дот выиграет, если выбросит не меньше a очков. Вероятность этого равна (6 - (a-1)) / 6. Поскольку a принимает всего 6 значений, ответы можно просто вычислить вручную.B. Бегущий студент
Общее время, которое понадобится студенту, если он выйдет на i-й остановке, равно ti = bi + si, где bi = xi / vb -- время, которое он проедет на автобусе, а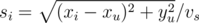 -- время, которое он пройдет от остановки пешком. Нужно выбрать индексы с минимально возможным ti, а среди них -- индекс с минимальным si, то есть, с максимальным bi, то есть (поскольку координаты остановок упорядочены) с максимальным i.
-- время, которое он пройдет от остановки пешком. Нужно выбрать индексы с минимально возможным ti, а среди них -- индекс с минимальным si, то есть, с максимальным bi, то есть (поскольку координаты остановок упорядочены) с максимальным i.Из-за возможных проблем с точностью условие ti = tj нужно записывать в виде |ti - tj| < ε для достаточно малого ε.
C. Числа Хексадесимал
Полный перебор чисел от 1 до n не пройдет по времени.Заметим, что все хорошие числа состоят из не более, чем 10 цифр, а каждая цифра равна 0 или 1. Значит, нужно проверить 210 бинарных строк. Каждая из них является числом от 1 до 210 - 1 в двоичной записи. Получаем такой алгоритм: для каждого числа от 1 to 210 - 1 запишем его двоичную запись, прочитаем ее так, как будто бы она была десятичной, и сравним результат с n.
D. Сколько деревьев?
Пусть tnh -- число бинарных деревьев поиска высоты h на n вершинах. Выведем рекуррентное соотношение на tnh. t00 = 1 (пустое дерево), а при i>0 ti0 = t0i = 0.Возьмем любое дерево высоты h на n вершинах. Пусть в корне записано число m, 1 ≤ m ≤ n. Левое поддерво является бинарным деревом поиска на m-1 вершине, а правое -- на n-m вершинах. Максимум из их высот должен быть равен h-1. Рассмотрим два случая:
1. Высота левого поддерева равна h-1. Таких деревьев tm - 1, h - 1. Правое поддерево в этом случае может иметь любую высоту от 0 до h-1 -- всего таких деревьев
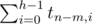 . Поскольку правое и левое поддеревья мы выбираем независимо, получаем
. Поскольку правое и левое поддеревья мы выбираем независимо, получаем 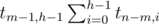 вариантов.
вариантов.2. Высота левого поддерева меньше h-1. Таких деревьев
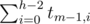 ; правое поддерево в этом случае должно иметь высоту h-1, и всего получается
; правое поддерево в этом случае должно иметь высоту h-1, и всего получается 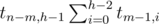 вариантов.
вариантов.Итак, рекуррентная формула такая:
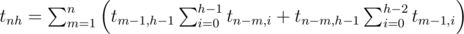 .
.Значения tnh вычисляются при помощи динамического программирования. Ответ на задачу --
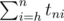 .
.E. Интересный граф и яблоки
Забавное кольцо состоит из n вершин и n ребер. Если есть еще какое-то ребро, кроме этих n, то вершины, которые оно соединяет, принадлежат более, чем одному циклу. Итак, интересный граф -- это просто забавное кольцо.Граф является забавным кольцом если и только если выполнены следующие условия:
A1. Степерь каждой вершины равна 2.
A2. Граф связен.
Теперь выясним, когда граф не является забавным кольцом, но может быть приведен к такому виду добавлением ребер. Очевидные необходимые условия:
B1. m < n.
B2. В графе нет циклов.
B3. Степени вершин не превосходят 2.
Будем добавлять ребра так, чтобы эти условия сохранялись, а последовательность ребер была лексикографически минимальна. То есть, добавим ребро (i,j) такое, что:
1. i и j принадлежат разным связным компонентам. (Иначе нарушится B2).
2. Степени вершин i и j меньше 2. (Иначе нарушится B3).
3. Пара (i,j) лексикографически минимальна.
Посмотрим, что получится, когда мы больше не сможем добавить ребро. Поскольку циклов нет, каждая связная компонента -- дерево, и в нем найдется вершина степени меньше 2. Если есть две связные компоненты, то их можно соединить ребром, не нарушив условий B1-B3. Итак, граф связен, не имеет циклов, и степень каждой вершины равна 2. Это значит, что полученный граф -- простая цепь, и можно соединить ее концы, получив забавный цикл.
Итак, алгоритм:
1. Проверить условия A1-A2. Если они выполнены, вывести "YES" и 0.
2. Проверить условия B1-B3. Если они не выполнены, вывести "NO".
3. Вывести "YES" и n-m.
4. Добавить ребра описанным способом. При добавлении ребра (i,j) вывести "i j".
5. Найти вершины i и j степени меньше 2 (они могут совпасть, если n=1). Вывести "i j".











D хорошая задача, жалко что не успел решить(
Насчет задачи B - достаточно найти наибольшее число k, состоящее из 0 и 1 и меньшее n. Делается это просто - считываем наше число n как строку, и идем по ней с начала. Если встречаем 0 или 1, то ничего не делаем, иначе меняем все символы с позиции i до конца на '1'. Например: 200 => 111, так как первый символ 2 больше 1. Затем получившуюся строку рассматриваем как число в двоичной записи, переводим в десятичную и выводим в качестве ответа.
you maked good tutorial
author's solution of problem E is looks like the same with yours ;)
The first version of my solution was quite a mess, but when I started to write the explanation, I understood that it can be rewritten much clearer. The benefit of writing tutorials :)
Directly was meant in reference to calculating answers using dynamic programming to the type of question that is asked (number of trees with height not lower than a certain amount). Here is the main loop (the full solution is viewable in the "practice room").
for (int j = 0; j <= n - 1; ++j)
mem[n][h] += count(j, std::max(h - 1, 0)) * count(n - 1 - j, 0)
+ count(j, 0) * count(n - 1 - j, std::max(h - 1, 0))
- count(j, std::max(h - 1, 0)) * count(n - 1 - j, std::max(h - 1, 0));
Or for each partition of the vertices to the left and right subtrees, the number of trees with height not lower than h is equal to the number of trees with the height of the left subtree not lower than (h - 1) plus the number of trees with the height of the right subtree not lower than (h - 1) less the number of trees with both subtrees of height not lower than (h - 1). The latter term is subtracted, because we have double-counted the solutions with both subtrees of height not lower than h - 1.
It's similar to what everyone else has.
Yes, your first problem was with rounding. If you cast (double)x[i]/v1 all should be Ok.
Test #23 checks the condition "If such bus stops (with minimal time arrival) are multiple, choose the bus stop closest to the University".
3 3 1
0 1 4
4 4
Stops 2 and 3 have the same time, but the 3rd stop is closer to the university.
Hope this helps you,
Good luck!
Good Job~
bi=g[1]/b;
целочисленное деление - 3/2 = 1
bi=1.0*g[1]/b;
или
bi=double(g[1])/b;
Так же ты не проверяешь условие "Если таких остановок несколько, то выберите ту, от которой расстояние до университета наименьшее". Это 23й тест.
Надеюсь переполнения переменных тоже нигде не будет, хотя как знать...
Нет.
3 3 1
0 1 4
4 4
В этом тесте время до 2 и 3 одинаково, но третья остановка ближе.
А здесь "bi=g[i]/b;" тоже исправил?
bi=g[i]/b;
надо заменить на bi = 1.0*g[i]/b;
bi=g[i]/b;
надо заменить на bi = 1.0*g[i]/b;
si=sqrt(((g[i]-x)*(g[i]-x)*1.0)+(y*y*1.0))/c;
надо сначала умножать на 1.0, но лучше просто объявить все переменные даблом.
tnh -- число бинарных деревьев поиска высоты h на n вершинах
Вычисляется по выведенным рекуррентным соотношениям.
Что именно непонятно?
example:
N = 101003021
X = 101001111
so, answer = 335
Problem E if input data ocuur a situation like this: n = 8 m = 9 1 2 2 3 3 1 3 4 4 5 5 6 6 4 is it yes?
in problem D tutorial.
neither of the 2 cases takes a height where height of left subtree or right subtree is greater than h-1.
why isn't this possible that there may be cases where either the LS or RS has height greater than h?
Can anyone please tell...
You are deriving recursive formula for a tree with n nodes and max height h in the current step. This n and h vary from (0..N) and (0..N) while calculating the dp table. When you have considered the tree with max height h then its left subtree can have max height h — 1 only.
Later you add up values in the dp table for trees of heights of (H..N).
yes .. i understood the rest part but where in the question it was mentioned that
height can't be greater than h.. it is written in the question that height can't be
lower than h but tutorial solve the question by taking max height upto h not more
than that .. here is the difference i was mentioning ..
otherwise the question is just similar of finding optimal binary search tree
Here we are solving for a general n and h. Not the ones mentioned in the question. We are summing up over all the possible subtrees which will have height less than h again because we are considering the tree with max height h.
In problem D, in case 2 of the above solution, shouldn't the height of the left subtree be less than h and not h-1 ?
Height of the left subtree — less than h-1. Height of the right subtree — exactly h-1 (otherwise height of the whole tree is less than h).
For E, a graph with multiple separated funny rings couldn't be an interesting graph?
A funny ring must visit every vertex of the graph. The English translation of the problem statement may be ambiguous...
Thanks
Got it
Al