slycelote's blog

Codeforces Beta Round #9 tutorial
By slycelote, 15 years ago, In English

A. Die Roll

If the maximum of Yakko's and Wakko's points is a, then Dot will win, if she has not less than a points. So the probability of her win is (6 - (a-1)) / 6. Since there are only 6 values for a, you can simply hardcode the answers.

B. Running Student

It is simple to calculate the time ti that the Student will need, if he gets off the bus at the i-th stop: ti = bi + si, where bi = xi / vb is the time he will drive on the bus, and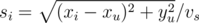 is the time he will need to get from the i-th stop to the University. We need to choose indices with minimal possible ti, and among them - the index with minimal possible si, that is, with maximal bi, that is (since the coordinates of bus stops are already ordered) with maximal i.

Note that due to precision issues, you should be careful when you compare ti: the condition ti = tj should be written in the form |ti - tj| < ε for some small ε.

C. Hexadecimal's Numbers

Brute force solution, when you try each number from 1 to n, will not fit into the time limit.
Note, however, that all good numbers have at most 10 digits, and each of the digits is 0 or 1. That is, there are at most 210 binary strings to check. Each of these strings is a number from 1 to 210 - 1 in binary representation. So the algorithm is the following: for each number from 1 to 210 - 1 write its binary  representation, read it as if it was decimal representation and compare the result to n.

D. How many trees?

Denote by tnh the number of binary search trees on n nodes with height equal to h. We will derive a recurrent formula for tnh. For the base case note that t00 = 1 (empty tree), and ti0 = t0i = 0 if i>0.

Now take any binary search tree on n nodes with height equal to h. Let m be the number written at its root, 1 ≤ m ≤ n. The left subtree is a binary search tree on m-1 nodes, and the right subtree is a binary search tree on n-m nodes. The maximal of their heights must be equal to h-1. Consider 2 subcases:
1. The height of the left subtree is equal to h-1. There are tm - 1, h - 1 such trees. The right subtree can have any height from 0 to h-1, so there are 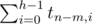such trees. Since we can choose left and right subtrees independently, we have 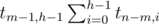variants in this case.
2. The height of the left subtree is less than h-1. There are 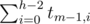such trees, and the right subtree must have height exactly h-1, which gives us totally 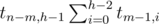variants.
So the recurrent formula is the following: .

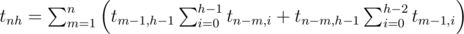All the values tnh can be calculated by dynamic programming. The answer, then, is .


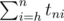E. Interesting graph and Apples

The funny ring consists of n vertices and n edges. If there is another edge except for these n, then the vertices it connects belong to more than one cycle. So, an interesting graph is just a funny ring.
A graph is a funny ring if and only if the following conditions hold:
A1. The degree of each vertex equals 2.
A2. The graph is connected.
 Now let's figure out when a graph is not yet a funny ring, but can be transformed into a funny ring by adding edges. There are obvious necessary conditions:
B1. m < n.
B2. There are no cycles.
B3. The degree of each vertex is not more than 2.
 Let's add edges so that these conditions were preserved, and the sequence of edges was lexicographically minimal. So, we add an edge (i,j) such that:
1. The degrees of i and j are less than 2. (Otherwise we would break B3).
2. i and j belong to different connected components. (Otherwise we would break B2).
3. The pair (i,j) is lexicographically minimal.
 Let's see what we have when we can't add edges anymore. Since there are no cycles, each connected component is a tree, and therefore has at least one vertex with degree less than 2. If there are two connected components, then they could be connected by an edge without breaking B1-B3. So the graph is connected, has no cycles, and the degree of each vertex is not more than 2. This means that the obtained graph is just a walk and we can connect its end points to obtain a funny ring.
 
 To summarize, the algorithm is the following:
 1. Check if A1-A2 hold. If yes, output "YES" and 0.
 2. Check if B1-B3 hold. If no, output "NO".
 3. Output "YES" and n-m.
 4. Add edges as described. When the edge (i,j) is added, output "i j".
 5. Find the only vertices i and j with degree less than 2 (they can be equal if n=1). Output "i j".
  • Vote: I like it
  • +7
  • Vote: I do not like it

Comments Comments (32)
| Write comment?
15 years ago, # |
  Vote: I like it 0 Vote: I do not like it
Thanks! =)
→ Reply
15 years ago, # |
  Vote: I like it 0 Vote: I do not like it

you maked good tutorial

author's solution of problem E is looks like the same with yours ;)

→ Reply
  • 15 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it
    Thanks!
    The first version of my solution was quite a mess, but when I started to write the explanation, I understood that it can be rewritten much clearer. The benefit of writing tutorials :)
    → Reply
15 years ago, # |
  Vote: I like it +1 Vote: I do not like it
in Problem D, we can calculate via dynamic programming the number of trees with n vertices and height not lower than h directly by using inclusion-exclusion.
→ Reply
  • 15 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it
    My algorithm is a bit different from yours, my program computes the number of tree with N nodes and its height is exactly H through DP.
    → Reply
  • 15 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it
    Hey, can you explain the solution which uses inclusion - exclusion principle directly in Problem D.
    → Reply
    • 15 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Directly was meant in reference to calculating answers using dynamic programming to the type of question that is asked (number of trees with height not lower than a certain amount). Here is the main loop (the full solution is viewable in the "practice room").

      for (int j = 0; j <= n - 1; ++j)
      mem[n][h] += count(j, std::max(h - 1, 0)) * count(n - 1 - j, 0)
      + count(j, 0) * count(n - 1 - j, std::max(h - 1, 0))
        - count(j, std::max(h - 1, 0)) * count(n - 1 - j, std::max(h - 1, 0));

      Or for each partition of the vertices to the left and right subtrees, the number of trees with height not lower than h is equal to the number of trees with the height of the left subtree not lower than (h - 1) plus the number of trees with the height of the right subtree not lower than (h - 1) less the number of trees with both subtrees of height not lower than (h - 1). The latter term is subtracted, because we have double-counted the solutions with both subtrees of height not lower than h - 1.

      It's similar to what everyone else has.

      → Reply
15 years ago, # |
  Vote: I like it 0 Vote: I do not like it
In problem B, I want to know what is the testcase 6?
In the problem statement:
"The second line contains n non-negative integers in ascending order"
so my code read n integer and it fail in testcase 6 but after the contest when I changed it from integer to double I got wrong answer at testcase 23..
This means that testcase 6 contains double..

So, what?

Also I viewed the accepted code of other contestants, I found that it is the same logic of my code, I don't know why my code is wrong answer at testcase 23??

Thanks,
→ Reply
  • 15 years ago, # ^ |
      Vote: I like it +12 Vote: I do not like it

    Yes, your first problem was with rounding. If you cast (double)x[i]/v1 all should be Ok.

    Test #23 checks the condition "If such bus stops (with minimal time arrival) are multiple, choose the bus stop closest to the University".

    3 3 1
    0 1 4
    4 4

    Stops 2 and 3 have the same time, but the 3rd stop is closer to the university.

    Hope this helps you,

    Good luck!

    → Reply
  • 15 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it
    wrong EPS?
    → Reply
    • 15 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it
      This problem doesn't need high precision and can be accepted without eps.
      → Reply
15 years ago, # |
  Vote: I like it 0 Vote: I do not like it
I'm quite agree with you on that writing a tutorials can make you feel much clearer.
→ Reply
15 years ago, # |
  Vote: I like it +1 Vote: I do not like it
The solution of E is very nice~
Good Job~
→ Reply
15 years ago, # |
  Vote: I like it +3 Vote: I do not like it
Another solution to prob C that runs in O(logN) is to take the maximum number X, formed only from '0's and '1's, that is smaller than N. Now we can treat X as in base 2 and the answer is it converted to base 10.
example:
N = 101003021
X = 101001111
so, answer = 335
→ Reply
  • 15 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it
    Why the complexity of this solution is O(logN)? I can see the solution with comlexity O(L), where L is the length of input string.(sorry for bad English)
    → Reply
    • 15 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it
      it's the same thing: log10(N) = L
      → Reply
      • 15 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it
        Oh, i thought that you mean log2N
        → Reply
        • 15 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it
          It's still the same, because log2(N) = log10(N) * log2(10). The difference is just a constant log2(10), thus it doesn't matter in complexity.
          → Reply
13 years ago, # |
  Vote: I like it 0 Vote: I do not like it
For problem C there is also an other approach. Read the number as a string. For each letter you make the follwing decision: If the number is greater than one, than all the other numbers in binary representation will also be one, otherwise if it is zero, the number representation is zero, and if it is one, it is one.
→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem E if input data ocuur a situation like this: n = 8 m = 9 1 2 2 3 3 1 3 4 4 5 5 6 6 4 is it yes?

→ Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

in problem D tutorial.

neither of the 2 cases takes a height where height of left subtree or right subtree is greater than h-1.

why isn't this possible that there may be cases where either the LS or RS has height greater than h?

Can anyone please tell...

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    You are deriving recursive formula for a tree with n nodes and max height h in the current step. This n and h vary from (0..N) and (0..N) while calculating the dp table. When you have considered the tree with max height h then its left subtree can have max height h — 1 only.

    Later you add up values in the dp table for trees of heights of (H..N).

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      yes .. i understood the rest part but where in the question it was mentioned that

      height can't be greater than h.. it is written in the question that height can't be

      lower than h but tutorial solve the question by taking max height upto h not more

      than that .. here is the difference i was mentioning ..

      otherwise the question is just similar of finding optimal binary search tree

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Here we are solving for a general n and h. Not the ones mentioned in the question. We are summing up over all the possible subtrees which will have height less than h again because we are considering the tree with max height h.

        → Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem D, in case 2 of the above solution, shouldn't the height of the left subtree be less than h and not h-1 ?

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Height of the left subtree — less than h-1. Height of the right subtree — exactly h-1 (otherwise height of the whole tree is less than h).

    → Reply
»
5 months ago, # |
  Vote: I like it 0 Vote: I do not like it

For E, a graph with multiple separated funny rings couldn't be an interesting graph?

→ Reply
  • »
    »
    5 months ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    A funny ring must visit every vertex of the graph. The English translation of the problem statement may be ambiguous...

    → Reply
»
5 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Thanks

→ Reply
»
5 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Got it

→ Reply
»
5 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Al

→ Reply