Problem A. Epic Game.

Author's solution: http://pastebin.com/zRiQwy6u

It's enough just to model the described game to solve this problem. You can search a greatest common divisor in any reasonable way.

Problem B. Before Exam.

Author's solution: http://pastebin.com/kBjCwiiD

Let's consider solution of the task for maximum level of profience (for minimum level solution is similar). It's clear that maximum level can be reached either in a card that has fallen one somebody's lot already or in a card about that we know nothing. In the first case we can just calculate levels of profiency for all cards from input and choose maximal level. The second case is more tricky. Let's sort all the theorems that weren't mentioned in cards from input in order of non-increasing of profiency's level. It's obvious that sought-for card consists of first 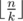theorems in sorted list. This case is possible if the number of different cards mentioned in input is stictly less than k. For example, in the test

3 2
1 2 3
2
1
2

we can't consider a card containing third theorem because both examination cards are already known.

Problem C. Education Reform

Author's solution: http://pastebin.com/eZhJYGpC

This problem can be solved by dynamic programming. Let's sort all subjects in order of complexity's non-increasing. Let d <  / span > [ < spanstyle = "" > i <  / span > ][ < spanstyle = "" > j <  / span > ][ < spanstyle = "" > z <  / span > ] is the greatest summary number of exercises, that can be given, if timetable contains exactly z subjects from among of first i subjects (in order of sort), involves ith subject and number of exercises in ith subject is equal to a_i + j. Recurrent correlations are based on search of subject that will occupy ( < spanstyle = "" > z <  / span >  - 1)th day in timetable.

For restoration of answer you should save source numbers of subjects.

Asymptotic complexity is O(m²·n·max(b_i - a_i)).

Problem D. String Transformation

Author's solution: http://pastebin.com/puGK1WYh

If lengths of input strings aren't equal, we can at once output "-1 -1" and complete execution of a program. Otherwise let number n is equal to the length of input strings.

Let's iterate through the number i. We should find (in O(1)) the such smallest number j, that substing b[0... n - i - 1] can be represented as a[i + 1... j - 1] + r(a[j... n - 1]). In order to do that, let's calculate the prefix function (p[i]) for string s₁ = r(a) + ' 0' + b and z-function (z[i]) for string s₂ = b + ' 0' + a. It's clear that for fixed i value of j is equal to n - p[2n - i - 1], and substrings a[i + 1... j - 1], b[0... j - i] must coincide at that (1). The last condition can be easily verified through using of calculated z-function. You can also trivial prove the next statement: if the property (1) is not satisfied by fixed i for the chosen j, then it will not meet for bigger j.

Asymptotic complexity is O(n).