Задача A. Эпическая игра (автор - dudkamaster).
Авторское решение: http://pastebin.com/zRiQwy6u
В этой задаче достаточно было просто промоделировать описанную игру. Искать наибольший общий делитель можно любым разумным способом.
Задача B. Перед экзаменом (автор - Serega).
Авторское решение: http://pastebin.com/kBjCwiiD
Рассмотрим решение задачи для максимального уровня знаний; для минимума задача решается аналогично. Понятно, что максимальный уровень может достигаться либо на билете, который уже попался кому-то из студентов, либо на билете, точное содержание которого нам ещё не известно. Для анализа первого случая можно попутно с чтением входных данных подсчитывать уровни знаний по билетам и выбирать максимальный из них. Второй случай хитрее. Отсортируем все теоремы, не вошедшие в другие билеты, по невозрастанию уровню знаний. Понятно, что искомый билет будет состоять из первых 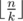 теорем в этом списке. Однако здесь возникает один очень важный случай, которого и не учитывало авторское решение: для того чтобы такая ситуация была реализуема, необходимо, чтобы количество различных известных нам билетов было строго меньше общего числа билетов. Эту ситуацию демонстрирует, например, тест
теорем в этом списке. Однако здесь возникает один очень важный случай, которого и не учитывало авторское решение: для того чтобы такая ситуация была реализуема, необходимо, чтобы количество различных известных нам билетов было строго меньше общего числа билетов. Эту ситуацию демонстрирует, например, тест
1 2 3
2
1
2
Мы не можем рассматривать билет, включающий в себе теорему №3, поскольку уже знаем содержание обоих билетов, которые будут на экзамене.
Асимптотическая сложность решения - O(n(q + log(n)).
Задача C. Реформа образования (автор - Serega).
Авторское решение: http://pastebin.com/eZhJYGpC
Данная задача решается при помощи динамического программирования. Отсортируем все предметы в порядке неубывания сложности. Пусть d[i][j][z] - наибольшее суммарное число упражнений, которое можно задать, если расписание содержит ровно z предметов из числа первых i (в отсортированном порядке), включает в себя i-ый предмет, а количество упражнений по i-ому предмету равно ai + j.
Рекуррентные соотношения основаны на переборе предмета, который будет стоять в расписании в z - 1 день. Для восстановления ответа необходимо сохранить исходные номера предметов, а при вычислении динамики - сохранять предков.
Асимптотическая сложность решения - O(m2· n· max(bi - ai)).
Изначально в этой задаче было немного другое условие, связанное с современной российской системой образования, однако оно было признано, цитирую, "неполиткорректным".
Задача D. Преобразование строки (автор - Serega).
Авторское решение: http://pastebin.com/puGK1WYh
Если длины входных строк не равны, сразу выведем "-1 -1" и завершим программу. Иначе положим число n равным длине входных строк.
Будем перебирать число i. Научимся за O(1) понимать, для какого наименьшего j подстроку b[0... n - i - 1] можно представить в виде a[i + 1... j - 1] + r(a[j... n - 1]). Для этого посчитаем префикс-функцию (p[i]) для строки s1 = r(a) + '\0' + b и z-функцию (z[i]) для строки s2 = b + '\0' + a. Понятно, что для фиксированного i искомым значением j станет n - p[2n - i - 1], при этом подстроки a[i + 1... j - 1] и b[0..j - i] должны совпадать (1). Последнее утверждение несложно проверить, используя подсчитанную z-функцию. Также тривиально доказательство того факта, что если при фиксированном i свойство (1) не выполняется для выбранного нами j, то оно не выполнится и для больших j.
Асимптотическая сложность решения - O(n).
Задача E. Другая реальность (автор - Kenny_HORROR).
Разбор размещён здесь.











Проверка того, что C следующего предмета больше чем C текущего.
Т.е. dp[i][j][xj-aj] - это суммарное количество заданий за i первых дней, если в i день мы поставим предмет j, и по нему поставим xj заданий. Тогда если c[j] < c[m], то dp[i+1][m][xm-am] = min(dp[i+1][m][xm-am], dp[i][j][xj-aj] + xm).
При итерационной реализации куда удобнее считать, что подзадачи для всех предметов, которые могут нам понадобиться, уже решены. Сортировка и даёт нам такой порядок предметов. Вполне возможно, что в этой задаче могут быть и другие подходы.
Коль решение задачи было изменено, отсюда изменяется и условие... Изменилось оно в том, что стало непонятно (и это стало важно), одинаковы ли билеты, в которых вопросы поставлены в разном порядке (например в тесте 2 есть билеты "2 3" и "3 2").
UPD. Этот коммент можно не читать
Помню, на Тимусе была задача 1450, а ее пофиксили потом...
Префикс и z-функцию мы используем уже после того, как зафиксировали начало (число i). Поскольку эти массивы были подсчитаны заранее, мы можем получить интересующую нас информацию за O(1). А сам префикс действительно можно перебирать обычным циклом, просто добавляя к нему по одному символу строки a и проверяя, что именно этот символ стоит в соответствующей позиции строки b.
Although this is a unreated round .. I am also get experience in this round ..
PS: I think Problem D is a good problem and it will have many many different solution.
what's the meaning of the z-function?
is it same with prefix function?
Getting 'Denial of Judgement' error on my submission of Education Reform problem.
Any suggestions?
P.S. Code is a bit long