Приглашаем всех школьников принять участие в олимпиаде по
программированию. Контест доступен
по ссылке http://judge.mipt.ru/cgi-bin/new-client?contest_id=201112 до
10 января. В данный момент в контесте 16 задач, постепенно
будут добавляться новые. Олимпиада проводится по кировской системе на
Ejudge сервере. Будут задачи разного уровня от самых простых до совсем
сложных, чтобы всем было интересно.
Победители получат призы и сувениры от факультета и спонсоров.
Составителями контеста являются тренеры и часть команды
mipt_waterogers. Все мы являемся аспирантами и выпускниками ФУПМ.
Желаем успехов и надеемся, что задачи вам понравятся!
P.S. Подробнее про систему Ejudge можно прочитать на judge.mipt.ru
программированию. Контест доступен
по ссылке http://judge.mipt.ru/cgi-bin/new-client?contest_id=201112 до
10 января. В данный момент в контесте 16 задач, постепенно
будут добавляться новые. Олимпиада проводится по кировской системе на
Ejudge сервере. Будут задачи разного уровня от самых простых до совсем
сложных, чтобы всем было интересно.
Победители получат призы и сувениры от факультета и спонсоров.
Составителями контеста являются тренеры и часть команды
mipt_waterogers. Все мы являемся аспирантами и выпускниками ФУПМ.
Желаем успехов и надеемся, что задачи вам понравятся!
P.S. Подробнее про систему Ejudge можно прочитать на judge.mipt.ru











Засчитывается последняя отправка, и результат известен только по концу соревнования?
То есть обычная "старая" система для школьников?
При вводе реальной даты рождения система не приняла входные данные - сообщила, что данные о дате рождения не корректны, пришлось сбросить эдак лет 40... :)
ะั ััะฟะตัะฝะพ ะทะฐัะตะณะธัััะธัะพะฒะฐะฝั
В задаче virus вообще условие само себе противоречит. А при попытке сдать эту задачу вылетела ошибка "Недоспустимый символ." Задал вопрос, ответа ещё не было.
В задаче, где нужно написать функцию, вообще не сразу понятно что нужно посылать, да и кажется глупо так строить задачу.
И да, не приятно читать задачи, которые не единообразно отформатированы.
но вообще они интересные
При попытке сдать j выпала ошибка "wrong symbol", попытался перелогиниться - меня туда больше не пускает, кнопки восстановления пароля тоже нет. Печаль.
UPD: Кто-нибудь знает, кому можно написать по этой проблеме?
По-моему нехорошо обсуждать задачи текущего контеста, причем ещё и с призами.
по мойму обсуждать нехорошо, когда обсуждается решение или идея решения, а тут я просто упомянул n! идентефицировать решение и идею по этому факту просто нереально
скорее, бурление говн поднялось не из-за того, что я что-то спросил, а из-за того что спросил yahooo, а не кто-то другой
Иногда и такой подсказки достаточно, чтобы догадаться до решения.
в таблице результатов уже два "Бориса Моисеева" - не к добру это(
Это я по криворукости остался без пароля, пришлось регистрировать новый, по моей просьбе они скрыты =)
UPD: получается не совсем по моей просьбе, и скрыты они у всех участников вне конкурса.
А вообще организаторы молодцы - правильно сделали, что оставили в таблице только школьников, ведь, как я понимаю, олимпиада не в последнюю очередь носит и профориентационный характер с далёким прицелом на отбор лучших к себе в ВУЗ.
олимпиада завершена. будет ли разбор или как решалась задача египет?
Скорее всего мы откроем для скачивания решения жюри. Что-то более подробное не гарантирую. Основные идеи Египта: 1) по простому модулю числа Ф-чи зацикливаются либо за p-1 (если 5 вычет), либо за 2(p+1), если невычет. Само собой, простые меньше или равно 5 надо рассмотреть отдельно 2) Если по модулю p^k последовательность Ф-чи зациклилась за t шагов, то по модулю p^{k+1} зациклится за t*p. Дальше КТО, и аккуратный подсчет башни по модулю.
конечно более интересно: дальше КТО (что это?) и как считать саму башню
P.S. КТО-это наверное китайская теорема об остатках?
КТО это видимо китайская теорема об остатках
да, конечно, китайская теорема об остатках. Считать башню по модулю периода тоже надо с помощью КТО и теоремы Эйлера (применяя ее рекурсивно). Нужно только аккуратно разбирать случай, когда основание очередной степени не взаимопросто с очередным модулем (там и пригодится КТО). http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%AD%D0%B9%D0%BB%D0%B5%D1%80%D0%B0_%28%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D1%87%D0%B8%D1%81%D0%B5%D0%BB%29 http://ru.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BE%D0%B1_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%B0%D1%85
Упрощенный пример: Если (a, m) = 1 и (b, φ(m)) = 1, то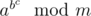 равно
равно 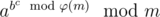 равно
равно 
Как решать про треугольник и круг, кроме как разбирать все случаи?(принципиально не стал писать)
Я пробегался по горизонтальным линиям с каким-то шагом и смотрел отрезки треугольника и круга, которые пересекаются с текущей прямой. Суммировал площадь пересечения на линиях и получал ответ с некоторой точностью.
А я разобрал все случаи, и когда разобрал, как-то стало немного лень писать :\
можно свести задачу к площади пересечения 3-х полуплоскостей и 3 "углов" с окружностью. Почти не надо разбирать никакие случаи, только писать достаточно трудно...
А я писала вообще жутко просто — использовала идею обычной площади многоугольника (ту, что суммирует ориентированные площади (векторные произведения в обычном случае)), получилось просто и без частников (только одна проверка была), поэтому я даже удивилась, что в задаче треугольник, т.к. моё решение не меняется от увеличения кол-ва вершин, а асимптотика линейная
Я решал именно так, банально, но муторно: геометрически, разбирая все возможные случаи, и что интересно решил верно. Вот только задача не прошла 12 тестов из-за моей невнимательности: я в одном случае вместо площади пересечения вывел площадь той части, которая лежит вне круга, и эту ошибку сумел найти только сейчас, посмотрев тесты этой задачи.
Можно заодно с решениями жюри и архивчик тестов открыть, в частности по Египту? Сильно интересно, что же там за вторая половина была.
Эгегей! Есть кто живой?
не уверен, что выложим тесты. Что касается египта, то могу прислать на почту, это моя задача.
Скинул в личку мэйл, не могли бы прислать?
Есть ли решение задачи про роботов, не используя поток? Я практически уверен, что нет, но мало ли.
я писал куна.
не знаю правильных решений, кроме потока
по сути кун делает тоже самое что и поток. А именно: нужно найти наибольшее паросочетание, но у каждой вершины будет не по одной соответствующей ей из другой доли, а по две. таким образом, если у каждой вершины из каждой доли будет по две вершины из другой доли, то можно утверждать что мы покрыли данный двудольный граф циклами.
да, я понял, это верно
можете показать код?
http://pastie.org/3382522
в этой задаче разбор случаев упорно не проходил всего один тест
не разобрали что-то видимо, у меня прошел