Здравствуйте!
Не так давно закончился пятый тур SnarkNews winter series — 2012. Поэтому, наверное, уже можно обсуждать задачи? У многих участников задача D — Triangles and circles не зашла с первого раза.
Мне бы очень хотелось узнать, как её решали другие участники. Если где-нибудь уже есть разбор этой задачи, прошу прощения, не нашел. Буду очень благодарен, если кто-то поделится ссылкой на него или напишет, как делал.
К сожалению, я пока так и не смог преодолеть в дорешке барьер WA 5 :)
Решить её пытался следующим образом:
Проверка условия
можно ли треугольник со сторонами a, b, c поместить внутрь окружности радиуса r так, чтобы все его точки лежали внутри или на границе окружности.
1. Если треугольник остроугольный
Т.е., если выполняется условие:
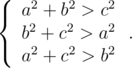
В этом случае треугольник можно поместить внутрь окружности, если радиус описанной окружности будет не больше радиуса заданной окружности:
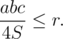
Площадь S найдем по формуле Герона:
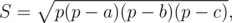
где
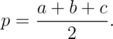
Подставив, получим исходное неравенство в следующем виде:
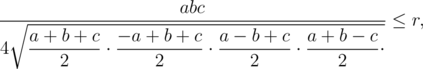
что равносильно
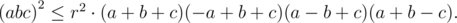
2. если треугольник не остроугольный
Очевидно, что треугольник поместится в случае, если половина его наибольшей стороны будет не больше, чем радиус окружности, т.е.
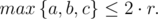
Определение максимального числа возможных пар
Я делал следующим образом:
Представим задачу в виде графа, в котором есть вершины двух типов (треугольники и окружности), где связь характеризуется возможностью помещения треугольника в окружность.
- Составим списки смежности вершин одного типа с другими.
- Среди вершин одного типа находим вершину с наименьшей степенью.
- Затем перебираем смежные с ней вершины и находим там с наименьшей степенью.
- Удаляем ребро, которое соединяет эти вершины вместе с самими вершинами. Следовательно, удаляются ребра, которые исходили из этих вершин. И увеличиваем ответ на 1.
- Повторяем шаги 2 — 4 пока остаются ребра.
Заключение
Скажите, пожалуйста, где и что я делаю не так. Вот мой горекод, который падает с WA 5.
Спасибо!










