A. Письмо
Чтобы найти наименьший прямоугольник, содержащий картинку, переберем все пары (i,j), для которых j-й символ в i-й строке равен '*', найдем минимальные и максимальные значения i и j среди этих пар. Искомый прямоугольник — [imin, imax] × [jmin, jmax].B. Юный фотограф
Сначала найдем пересечение всех отрезков. Для этого обозначим самый правый из левых концов отрезков через m, а самый левый из правых концов — через M. Пересечение всех отрезков есть отрезок [m,M] (или пустое множество, если m>M). Теперь определим ближайшую точку из этого отрезка. Если x0 < m, то ближайшая точка — m, и ответ — m - x0. Если x0 > M, то это M, и ответ — x0 - M. Если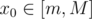 , это x0, и ответ — 0. Если m>M, то ответ — -1.
, это x0, и ответ — 0. Если m>M, то ответ — -1.C. Четыре отрезка
Наверняка есть много способов решить эту задачу. Следующий алгоритм кажется достаточно простым.Сначала сосчитаем число различных концов отрезков. Если оно не равно 4, то отрезки не могут образовывать прямоугольник, так что ответ "NO". Далее, вычислим максимальную и минимальную координаты этих четырех точек: xmin, xmax, ymin, ymax. Если xmin = xmax или ymin = ymax, то даже в случае, когда отрезки образуют прямоугольник, его площадь равна нулю, поэтому здесь мы также выводим "NO".
Теперь, если отрезки действительно образуют прямоугольник, то мы знаем его вершины: это (xmin, ymin), (xmin, ymax), (xmax, ymin) и (xmax, ymax). Мы можем просто проверить, что каждая сторона этого прямоугольника присутствует во входных данных. Если это так, то ответ "YES", иначе "NO".
D. Два пути
Возьмем любую пару непересекающихся путей. Поскольку Флатландия связна, найдется третий путь, соединяющий эти два. Удалим дорогу из этого третьего пути. Флатландия разобьется на две компоненты — одна содержит первый путь, а другая — второй. Это наблюдение подсказывает нам алгоритм: переберем все дороги; для каждой дороги удалим ее, найдем самый длинный путь в обеих связных компонентах и перемножим длины этих путей. Самый длинный путь в дереве можно найти с помощью поиска в глубину из каждой висячей вершины.E. Верблюды
Назовем впадиной индекс j такой, что yj - 1 > yj < yj + 1. Горбы и впадины будем называть общим словом излом. Тогда должно быть ровно T = 2t - 1 изломов, первый из которых должен быть горбом.Обозначим через fnth количество способов продолжить верблюда с t изломами, оканчивающегося в точке (n,h), до конца (то есть до вертикали xN = N) так, чтобы общее число изломов стало равным T. Заметим, что:
1. fNTh = 1, если h=1,2,3,4. (Мы полностью нарисовали верблюда, и у него ровно T изломов)
2. fNth = 0, если 0 ≤ t < T, h = 1, 2, 3, 4. (Мы полностью нарисовали верблюда, но у него меньше T изломов)
3. fn, T + 1, h = 0, если 1 ≤ n ≤ N, h = 1, 2, 3, 4. (У верблюда уже больше T изломов).
Найдем рекуррентную формулу для fnth. Допустим, что t четно. Тогда последний излом был впадиной, и в данный момент мы движемся вверх. Мы можем продолжать двигаться вверх, тогда число изломов не изменится, и мы перейдем в одну из точек (n + 1, h + 1), (n + 1, h + 2), ..., (n + 1, 4). Мы также можем повернуть вниз, тогда число изломов увеличится на один, и мы перейдем в одну из точек (n + 1, h - 1), (n + 1, h - 2), ..., (n + 1, 1). Таким образом, получаем формулу
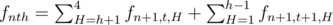 .
.Если t нечетно, то последний излом был горбом, и похожие рассуждения приводят нас к формуле
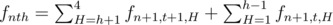 .
.Вычислим значения fnth с помощью динамического программирования. Теперь рассмотрим точку (2, h) в верблюде. Есть h-1 способов добраться до этой точки (можно начать в точках (1, 1), ..., (1, h - 1)), и f2, 0, h способов продолжить верблюда до конца. Таким образом, ответ на задачу —
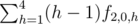 .
.










Задачу C я решал немного другим способом, в котором не требуется перебирать все стороны в итоге :)
При считывании каждого отрезка заносятся обе точки в множество dots, если отрезок вертикальный - в vertical, если горизонтальный - horizontal (проверяем ещё на вырожденность отрезка). Если все 3 множества в итоге имеют 4 элемента - получили то, что требуется.
typedef complex<int> point;
set<point> S;
But it doesn't work. I can't insert any element using S.insert();
Anyway. std::complex cannot be used with std::set, because it doesn't define operator<. Write your own struct or use std::pair.
D. Two Paths
same question on spoj.pl but 2 ≤ N ≤ 100000 any idea how to solve.https://www.quora.com/How-do-I-solve-SPOJ-Two-Paths-problem
7 years late -_-
10 years late =))
I believe my solution runs in $$$O(n\log{}n)$$$. There is a log factor because I am using sort(I believe I can get rid of it btw because I use it to pick the largest value and second-largest one in a vector). So in my solution, firstly I calculate the diameter of the tree using DP which means I obtain the answer for each node considering only nodes in its subtree in the tree rooted by an arbitrary node. Then, I use the rebooting technique of the tree following the order of the dfs. For each edge (u,v), I suppose it is cut and I calculate the diameter of the tree rooted by u but without the subtree rooted at v and since I have already calculated the diameter of the subtree rooted by v, I multiply these two values of diameters and keep the maximum result. Here is my code 74234280.
If you keep the diameters of the subtrees and then you make an idea like rerooting: dp in-out, we can reduce it to $$$O(n)$$$ because in rerooting it would only change $$$O(deg (v))$$$ heights of nodes, right?
We can solve this when we remove the information from the child to some root, at that moment it is as if the edge does not exist.
About the solution of problem E.
The first one must be a hump, also ** the last one must be a hump.**
So, fNth = 0, if0 ≤ t < T, h = 1, 2, 3.
BTW, when N + 2 < T, no camel with t humps exist, so the answer is 0.