150E - Замерзаем красиво
Идея:
Сделаем бинарный поиск по ответу. Пусть мы хотим проверить существование пути с медианой Mid.
Если ребро ≥ Mid положим его вес равным + 1, иначе - 1. Теперь надо проверить существование пути не отрицательного веса, у которго длина ≥ l и ≤ r. Назовем такой путь хорошим.
Подвесим дерево за какую-то вершину V.
Сначала предположим, что путь проходит через V. Затем удалим эту вершину и сведем задачу к нескольким меньшим.
Если в качестве вершины V выбирать центр дерева (такую вершину, что после подвешивания за нее, размер всех поддеревьев не превохсодит половины размера всего дерева), то таких шагов будет не более Log(N).
Т.е если мы сейчас научимся за O(F(N)) проверять наличие хорошего пути, то мырешим задачу за сложность O(F(N) * log2(N)).
Для начала научимся ее решать за O(NLog(N)). Для каждой вершины посчитаем ее глубину, стоимость пути от нее до корня, и первое ребро на пути от корня до нее. Вершины будем обрабатывать пачками, в одну пачку попадают вершины с одинаковым первым ребром. Это сделано чтобы все учтенные пути были простыми. Сначала для каждой вершины из пачки вычислим максимальную стоимость хорошего пути, начинающегося в ней, проходящего через корень, и заканчивающегося в вершине из уже обработанной пачки. В силу того, что мы обрабатываем вершины пачками, условие прохождения через корень выполнится автоматически. Построим дерево отрезков на массиве q[x] = максимальная стоимость пути длиной x начинающегося в корне. Тогда для нашей вершины искомая величина это просто максимум на отрезке с L - dep по R - dep. Затем после обработки всей пачки сделаем апдейты в дереве интервалов.
Чтобы получить АС нужно было очень аккуратно написать это решение (его сложность O(N * log3(N)) ~ 8 * 108 операций или заметить, что можно заменить дерево отрезков очередью с максимумом.
150D - Миссия непроходима
Правильное решение — динамика. Для удобства будем вычислять три динамики, каждая зависит от обеих других. Обратите внимание, что не смотря на это динамика — ациклическая.
Состояния:
Best[l][r] — лучший результат который можно получить на подстроке с l по r.
Full[l][r] — лучший результат который можно получить на подстроке с l по r, при этом удалив ее полностью.
T[l][r][Len] — лучший результат который можно получить на подстроке с l по r, чтобы в результате получился палиндром длины ровно Len и больше ничего.
Переходы:
Full[l][r]. Давайте посмотрим какой ход мы сделаем последним. Это будет удаление палиндрома какой-то длины len, причем c[len] ≥ 0. Какой результат мы в итоге получим? c[len] + T[l][r][len], где T[l][r][len] — это оптимальный способ оставить на отрезке только палиндром длины len.
Best[l][r]. Либо мы удалим отрезок целиком, либо существует буква, которую мы не трогали. Но тогда каждый удаляемый палиндром лежит либо строго слева либо строго справа от этой буквы. Другими словами можно решать задачу независимо для левой половины и правой. Получаем что либо Best[l][r] = Full[l][r] либо Best[l][r] = Best[l][m] + Best[m + 1][r] для какого-то m, l ≤ m < r.
T[l][r][len]. len = 0, len = 1 — два частных случая, которые надо рассмотреть отдельно. В общем же случае давайте посмотрим на самую левую букву. Она либо войдет в оставшийся в результате палиндром либо нет. Если нет, то переберем позицию m (l < m ≤ r) самой левой буквы которая войдет в ответ. Все что находится слева от нее необходимо полностью удалить, из оставшейся строки все еще нужно оставить палиндром длины len. Получили Full[l][m - 1] + T[m][r][len] (for l < m ≤ r). Аналогично для самой правой буквы. Если она не войдет в ответ, то мы целиком удалим какой-то суффикс нашего отрезка. Получаем T[l][m][len] + Full[m + 1][r] (for l ≤ m < r). Остался последний вариант: и самая левая и самая правая буквы войдут в ответ, но тогда они обязаны совпасть. Значит в случае когда s[l] = s[r] мы можем их обе оставить и набрать оптимально палиндром на 2 символа короче на отрезке с l + 1 по r - 1. Получаем последний переход T[l + 1][r - 1][len - 2] (if s[l] = = s[r]).
150C - Хитрый жук
Для каждого пассажира будем решать задачу независимо, затем просто выведем сумму результатов.
Для каждого маленького отрезка пути (перегон между соседними станциями) посчитаем матожидание заработка если мы не продадим билет на него.
Теперь, когда нам нужно решить задачу для пассажира едущего с L до R, на самом деле надо найти под отрезок с максимальной суммой.
Это можно сделать например при помощи дерева интервалов. Каждая вершина дерева покрывает какой-то отрезок массива с l по r. Будем в ней хранить следующие величины: префикс с максимальной суммой, суффикс с максимальной суммой, сумму на всем отрезке и просто лучший результат. Для отрезка длины 1 все эти величины вычисляются очевидным образом. И в то же время, зная все эти величины для обоих сыновей вершины, мы с легкостью можем пересчитать значения в нашей.
150B - Количество строк
У задачи есть два принципиально разных решения:
Построить граф, где ребра это позиции в строке, а ребро означает равенство символов. Тогда на позициях, оказавшихся в одной компоненте связности, должны стоять одинаковые буквы. Пусть e — количество компонент связности, тогда ответ в точности равен me.
Разобрать четыре случая:
- k = 1 или к > n ответ mn.
- k = n ответ m(n + 1) / 2.
- k mod 2 = 1 ответ любая строка вида abababab..., т.е. ответ m2.
- k mod 2 = 0 все символы в строке совпадают, т.е. ответ m.
150A - Победи или замерзни
Если Q — простое или Q = 1 то первый игрок уже выиграл.
Проигрышные позиции: p * q и p2, где p и q — простые.
Вполне очевидно, что из всех остальных позиций мы можем сделать ход в одну из проигрышных. Значит они выигрышные.
Остается лишь аккуратно проверить, что у нашего числа есть делитель удовлетворяющий условию проигрышности. Это можно сделать за O(sqrt(Q)) факторизовав наше число.
151B - Телефонные номера
Задача скорее техническая, нежели идейная. Требовалось аккуратно считать входные данные и по каждому номеру понять какого он типа. Затем вычислить глобальные максимумы для всех трех типов номеров. И, наконец, вывести в выходной файл имена всех людей, у которых количество номеров совпадает с оптимальным.
151A - Газировкопитие
Газировки хватит на gas = (K * L) / (N * l) тостов.
Лаймов хватит на laim = (C * D) / N тостов.
Соли хватит на sol = P / (p * N) тостов.
Итого ответ: res = min(gas, laim, sol).











В div1 B последние 2 случая перепутаны
Верно, Серега потом исправит
а в div2 E можно было использовать вместо дерева отрезков — поиск подотрезка массива с максимальной суммой? у меня решение не проходит на 2 тесте. Не могу понять проблема в выборе метода или где ошибся
1) C и D, упоминаемые в условии, могут быть разными для разных пассажиров.
2) Если дело не в предыдущем пункте, то наверно у тебя алгоритм за O(n*m) — для каждого пассажира проходим по всему его отрезку. Предполагалось решение за O(m*log(n)).
Спасибо, но у меня WA на 2 тест , до TL даже не дошло дело, никак не могу понять в чём дело. Вроде решал так же как описано в комментах, вот 1201221. Подскажите пожалуйста что не так, а то я чёто тупллю
В _m: 1) надо делить пополам не только первое слагаемое, а оба, 2) второе слагаемое надо делить на 100.
div2 D. Почему если к > n ответ m^n?
По условию рассматриваюдся подстроки заданной длинны, а таких нет.Значит любая строка подходит.
Объясните как были получены формулы ДП(динамического программирования) для задачи div1-D, так чтобы в будущем уметь их вывести в похожей задаче. На codechef'е была близкая к этой задача (http://www.codechef.com/OCT10/problems/STREDUC). В едиториале к ней (http://www.codechef.com/download/STREDUC.JPG) было сказано что задача требует "очень хороших навыков ДП...". Я думаю это была отмазка, просто авторы поленились расписать ход своих мыслей при получении формул ДП.
Теперь в тексте разбора можно прочитать подробное описание переходов.
Да, решение Е очень классное.
Мне интерестно, не решается ли она не так красиво с помощью Х-Л декомпозиции? Какие для этого предпосылки:
Задача не на дереве, а на отрезке решается с помощью БП и затем линейного прохода.
Х-Л декомпозиция превращает дерево в несколько отрезков и часто позволяет решить задачу так же, как на отрезке, с добавочным множителем logN.
В качестве примера — В ПТЗ задача была про разворот номеров на пути на дереве, которая решалась так же, как на отрезке (трипом), ну и плюс Х-Л.
Но, не смотря на все эти совсем не убедительные доводы, ничего похожего на решение на отрезке с очередью с максимумом по массиву частичных сумм, придумать не удалось:(. Any thoughts как это сделать или почему в данном случае такое сведение невозможно?
Строго ничего доказать не могу, но продолжая интуитивные соображения автора:
Под "просто обходом" имеется в виду обход, в котором хранятся сеты расстояний до всех потомков, которые сливаются от большего к меньшему, что приводит тоже к ответу в одной итерации БП за Nlog2N или что-то другое?
For 150B, i think if you give a "k > n case" in the sample , it will reduce lots of misunderstanding.
Can someone give a more detailed explanation for 150B in the cases when k%2=0 and k%2=1.Its not clear for me
Before we check whether k is odd or even(k%2 == 1 or k%2 == 0), we check following two conditions.
k = 1 or к > n, the answer is mn. k = n, the answer is m(n + 1) / 2.
So we know the current k is 0 < k < n
Let's look at the case when k%2 == 1 Let a = an arbitrary character from "m" possible characters. b = an arbitrary character other than "a" from "m" possible characters
If k is odd, a substring whose length is k out of following string is always a palindrome. String : abababababa Substring k=3 => aba or bab k=5 => ababa or babab ... you see the pattern. So we have (m * (m-1)) possible patterns. Now, also remember that a string consisting of same characters are also allowed. string : aaaaaaa substring k=3 =>aaa k=5 => aaaaa And we have "m" number of such strings.
So answer is m*(m-1) + m = m*(m-1+1) = m*m
Let's see what happens when k is even. If k is even, only allowed strings are the ones that consist of same characters. There are m such strings. So answer for (k%2 == 0) is m
Thanks for the explanation :)
I actually failed 150B because of case k > n, and I still don't understand why it is regard the same as k == 1.
case where k == 1 is trivial. The answer is all possible strings.
However, in case k > n, I think the answer should be 0 because you cannot make a SUBSTRING whose length is LONGER than the ORIGINAL string. Also, by definition, a substring is a part of a string, not extended version of a string.
Let's take an example. Let's say n == 5 and k == 7. You have strings made out of "m" selection of characters, and the strings' lengths are always 5. How can you possibly make a substring whose length is 7 from one of strings whose length is 5?
If I am wrong, please help me understand why all possible strings are regarded as palindrome when k > n.
All 0 k-substrings of any string is palindromes.
So any string is correct.
What do you mean by "0 k-substrings of any stirng" ?
Could you please explain with a litte bit more detail?
There are 0 substrings of length
k.All of them are palindromes because Any statement about empty set is truth
Thx.I get it now. :-)
http://en.wikipedia.org/wiki/Vacuous_truth
Let's solve your example (n = 5, k = 7) step by step. Let's check every possible string (let m be 2) if it satisfies the condition.
Let's look on string abaab. Condition is that every substring of length 7 of string abaab is palindrome. Set of such substrings S is empty, it's obvious. So the condition "every element x of S is palindrome" is true.
If you still don't believe me, let's look another way. If condition of type "every element a in set B satisfies condition C" is false, that means, that exists some element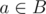 that don't satisfy condition C. In out example, if string abaab doesn't satisfy our condition, then there exist some substring x of our string, that x isn't palindrome. But you can't choose such x: there is no substring of length 7 in our string. So the proposition of that abaab doesn't satisfy condition is false. So this condition is true for abaab, so we have to include abaab to answer.
that don't satisfy condition C. In out example, if string abaab doesn't satisfy our condition, then there exist some substring x of our string, that x isn't palindrome. But you can't choose such x: there is no substring of length 7 in our string. So the proposition of that abaab doesn't satisfy condition is false. So this condition is true for abaab, so we have to include abaab to answer.
Such proof is correct for every string of length n on m-alhpabet, so answer is mn.
i like these problems, but that editorial for 151B is sort of ...
Hi everyone. For 150C can anyone explain details of the point 1 and 2 of this problem?
First lets use the linearity of expected value and solve task independently for each passanger.
For each path segment (route between neighboring stations) we calculate expected value of profit in case we do not sell a ticket for this segment. In case we sell it the expectation of profit is 0.
Can someone help me out with the graph approach of problem 150B, the other approach is straight forward but I can't wrap my head around the graph one, thanks!!
Refer to this link, its a similar problem. https://discuss.codechef.com/t/magical-strings-editorial/11926
Thanks sir ! Your Comments Really Help me alot
thank you GOD ..........your comment helped whole coder community alot
The markdown seems to be broken.
211135796
Div2 D, here is the first solution based on DSU.
what is Div2B , the logic is easy enough but it took me more than an hour just to get the output format right.