В связи с тем, что .masterhost продолжает держать opencup.ru и snarknews.info на серверах, доступных только с российского IP, выкладываю ссылки на первый и второй дивизионы ГП ICL:
http://158.250.33.215//team.cgi?contest_id=10174 — Division 1
http://158.250.33.215//team.cgi?contest_id=10184 — Division 2
Старт, как обычно, в 11-00. Этап будет учитываться в отборе на Чемпионат Урала.
Update:











Еще бы ссылки на таблицы результатов для болельщиков.
Где таблица?
http://158.250.33.215/~ejudge/res/res10174
Как решать B, C, F, G, I, K?
Расскажу как решать F. На контесте не сдали, забыли закомментить отладочный вывод за 3 минуты до конца и получили ВА1, но в дорешивании прошло. Идея такая: Найдем k такое, что pk ≤ n < pk + 1.
Заметим, что количества апельсинов на дереве равно pm - a[m - 1]pm - 1 - ... - a[0]p0. При этом a[i] равно либо 0, либо 1. Тогда если два дерева дают в сумме n то это один из трех случаев:
Рассмотрим каждый из них отдельно.
Складывая ответы для всех трех случаев получаем окончательный ответ.
Вот код на JAVA: http://pastebin.com/y8JXFUg9
B вот так сдали: Не сложно придумать ДПшку f(lx, ly, ux, uy) = solution, где solution — вектор времен (т.е. solution[1] — время когда ячейка с 1 освободится, solution[2] — когда 2я и т.д., если solution[i] = 0, значит iго числа не было в прямоугольнике) и solution лексикографически минимальный среди всех возможных вариантов, т.е. для каждого прямоугольника посчитать оптимальный разрез, чтобы в итоге получились времена solution.
Для расчета надо перебрать 4 варианта разреза — какой раньше будем делать — для каждого разреза получаются два прямоугольника в общем случае — sol1, sol2, чтобы померджить ответы надо просто sol1[i] | sol2[i].
Это будет что-то (n * m)3 и по памяти столько же. Так как числа solution[i] не большие, то можно в int по 3 числа засунуть, но это тоже получается много.
Можно заметить, что можно хранить только для минимального в прямоугольнике актуальное время (будет от 1 до 4), а для остальных хранить смещение по времени (от 0 до 4), т.е. получается на значение по 3 бита и в long long можно по 21-му числу запихать. Это уже получается (n * m)2 * (n * m) / 21. Такое зашло. Ну и там на самом деле делить на некоторую константу, потому что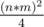 прямоугольников и еще не для всех считать надо.
прямоугольников и еще не для всех считать надо.
На туре не увидел, что в B динамика. Снимите мне 1000 рейтинга)
ХорошоВернул назад :)Наверное это плохо, когда из системы просто так исчезает 1000 очков рейтинга — всякие плохие спецэффекты возникнуть могут. Добавьте его мне.
Сумма рейтингов прилично убывает за каждый раунд. Например сумма изменений за 114 раунд чуть меньше -35000(оба дива).
Это новый способ борьбы с инфляцией рейтинга? :)
Спасибо! Это заслужено :)
Ой, как здорово, а можно мне снять 2016 рейтинга?
Нужна кнопка "уменьшить себе рейтинг до нижней границы дивизиона". Для борьбы с инфляцией — самое то! :-D
Так надо было сразу просить обнулить), а оставшийся рейтинг по-честному разделить)
Как решалась Н (точнее, как разбирать в ней частный случай k = 1) и кто до какого теста дошел в N?
В H можно написать например какой-то такой брут:
for(i=1;i<=max(a[1]-1,n-a[1]);i++)ans+=((a[1]-1)/i+1)*((n-a[1])/i+1);
cout<<ans-max(a[1]-1,n-a[1])+1<<endl;
a[1] тут позиция нашего единственного дерева.
Теперь заметим что различных пар среди ((a[1]-1)/i+1), ((n-a[1])/i+1) будет немного не смотря на то что i может быть очень большим. Тогда за одну итерацию будем считать какая получается пара и сразу сколько таких будет. Код
Ответ это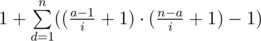 . Для
. Для 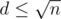 посчитаем втупую, а для больших разобьем на отрезки, где выражение под суммой постоянно, их будет
посчитаем втупую, а для больших разобьем на отрезки, где выражение под суммой постоянно, их будет 
opencup.ru по-прежнему недоступен. Можно ли выложить прямые ссылки ещё и на дорешивание?
http://158.250.33.215//team.cgi?contest_id=9911&locale_id=1
http://158.250.33.215/~ejudge/team.cgi?contest_id=9911
Как решается задача D??
Отсортируем машины по координате Х, т.е. по времени, за которое они доехали бы до моста, если бы других машин не было. Пусть время въезда каждой машины на мост будет time[i], а номер машины среди всех машин с таким же временем (ведь несколько машин могут заехать на мост одновременно) будет Num[i].
Рассмотрим теперь машину номер k. Если X[k] > time[k-1], то time[k] = X[k], Num[k] = 1. Иначе, если Num[k-1] < B, то time[k] = time[k-1], Num[k] = Num[k-1] + 1. Если же Num[k-1] == B, то time[k] = time[k-1] + 1, Num[k] = 1.
Ответ: time[N]
Как решалась задача L?
Можно было решить с помощью стэка — в нем будут хранится текущие потенциальные победители: Идем слева на право. Пусть мы рассматриваем машину i: выкидываем из стэка всех игроков, которых выигрывает машина i. Если стэк пустой или "ничья" у машины i с последним невыкинутым элементом стэка, то кладем i в стэк. В итоге стэк — это ответ.
Спасибо
В G зашло в дорешивании следующее:
1) Пусть time(X,Y) = INF, если игрок X не может поймать игрока Y, и максимальному времени, сколько Y может сопротивляться, если X может поймать Y. 2) Тогда пусть win(A) = time(A, B), если time(A, B) < time(C, A) (вроде как естественное условие, но может кстати и без него будет работать?..) и time(A, B) < time(C, B) (иначе C может "встать между A и B и добиться ничьей), и INF иначе. Аналогично для win(B) и win(C). 3) Тогда если среди win есть единственный минимум, то он и побеждает в игре для троих, иначе ничья.
Выглядит правдоподобно, но это далеко не первая итерация, и все предыдущие тоже выглядели правдоподобно :) Может у кого-то есть объяснение или более простое работающее решение?
о, что-то похожее на авторское =)
правда я делал сперва проверку "может ли участник скрыться на каком-либо цикле", то есть гарантированно не проиграть, а потом оперировал значениями, полученными в результате поисков в ширину, запущенными для каждого из игроков
alexey.enkov даже умеет доказывать корректность такого решения
думаю, что вряд ли существует что-нибудь попроще :)
Как считать ф-цию TIME? В ней нужно учитывать, что есть ещё враг, который может всё обломать? Вот рассмотрим например третий сэмпл: 3 3 1 2 1 3 2 3 1 2 3
time(ALICE,BOB)=1; time(ALICE,CEASER)=1; time(BOB,ALICE)=INF; time(BOB,CEASER)=1; time(CEASER,ALICE)=INF; time(CEASER,BOB)=INF;
win(ALICE)=1; win(BOB)=INF; win(CEASER)=INF; => ANS: ALICE
Где я не понял решения?
Ещё: как решалась задача Е(Фифекты Гечи), задача J(Острова) и задача N(Числа)?
J изи — обычный дфс, только состояние кроме текущей вершины еще знает, мост с какого острова использовали на предыдущем ходу.
Е — пусть мы что-то сделали и у нас получилось
a1 первых операций, a2 операций и.т.д.
min(ai) = 0, ибо можно каждое уменьшить на 1.
Ясно, каких операций меньше всего(0).
Из этого ясно, сколько всго операций.
Посчитаем, сколько тогда должно быть все остальных операций. Там получается уравнение вида,
ax = b, если решений нет, то сразу падаем.Осталось восстановить порядок, как делал я:
Скидаем в приоритетную очередь (номер, стартовое_количество), наверху — минимальное по кол-ву. Достаем очередной минимум на i-ом шаге: если стартовое кол-во < i — падаем, иначе выводим и увеличваем на k-1 стартовое_количество.
В этом сэмпле никто никого не может поймать — они же на цикле? Поэтому все time равны INF.
Считать time примерно так — построим ту часть графа, начинающуюся в вершине B, которая является деревом — т.е. как только мы доходим до цикла, помечаем эту вершину как "выход" и дальше не идём. В этой части есть ровно одна вершина, откуда стартует A — либо где он сейчас, либо где он появится. Подвесим часть за неё, тогда нужно на пути от B до корня понять, докуда B ещё может дойти, и из всех этих вершин найти самого глубокого ребёнка, считая глубину цикла INF.
Ну то есть, отвечая на второй вопрос — для подсчета time про третьего вообще забываем.
Задача E.
Пусть Ai — стартовое кол-во людей с i дефектом, а Bi — конечное. Di = Bi — Ai — разница между начальным и конечным значением.
Для начала проверим, чтобы сумма всех Di была равна нулю. Если это не так, то ответ -1. Если все Di равны нулю, то ничего делать не надо и ответ 0. Далее рассмотрим общий случай:
Пусть K — общее количество операций, которое мы совершили над нашим множеством. Ei — количество встреч людей без i-го дефекта.
Тогда для каждого человека должно выполняться следующее уравнение:
Ai + (m — 1) * Ei — (K — Ei) = Bi
Что преобразуется в:
Ei * m — K = Di . Тогда, Ei = (Di + K) / m
Теперь, для каждого человека нужно найти такое минимальное K > 0, чтобы (Di + K) делилось на m и (Di + K) / m >= 0. Для отрицательных Di, K равно Di, а для неотрицательных, найдем Div = Di / m + 1. Тогда Di + K = Div * m, K = Div * m — Di.
Среди всех людей найдем максимальное K. Теперь нужно проверить всем ли людям данный K подходит. Т.е. для всех людей (Di + K) должно делится на m. Если это не так, то ответ — 1. А заодно для каждого человека найдем уже финальное Ei.
Теперь мы знаем для всех — Ei и нам нужно оптимальным образом выполнить эти операции. Заведем очередь с приоритетами, где на вершине будет хранится человек с минимальным текущим Ai и которому еще нужно сделать операции Ei. Достаем человека. Если его текущее значение — кол-во проведенных операций < 0, то ответ -1. Иначе прибавляем ему значение m и если ему нужно сделать еще операции, то добавляем его обратно в очередь.
Расскажите, как решать B?
Наше решение. По-моему по коду все понятно
Спасибо. Да... что-то я ступил:(
Про задачу J
Кажется, правильный ответ NO. Мое AC-решение на opencup выдает YES. weak tests?!
Кажется, правильный ответ YES. Можно дойти таким образом: (1,1)->(1,2)->(1,3)->(1,4)->(1,3)->(1,2)->(2,2)->(2,1)->(3,1)->(4,1)->(4,2)->(4,3)->(4,4)
А, я перечитал второй sample. Я не понял задачу, но получил по ней Accepted :)
Оказывается, слово "подряд" означает "два раза последовательно" :-D
Как решалась К?
Во-первых, (это делать необязательно, но удобнее для дальнейших вычислений) избавимся от палиндромов четной длины, вставив через один какой-либо символ, не встречающийся в строке. После этого для всех i найдем количество палиндромов с центром в i. Ответ для запроса (x, y) равен сумме минимумов по отрезку запроса от длины палиндромов в текущей позиции и расстоянию до границ запроса :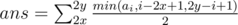 . Поскольку в левой части отрезка запроса берется минимум от ai и расстояния до левой границы, а в правой — до правой, поделим отрезок пополам и будем считать каждую часть отдельно. Левая часть для запроса:
. Поскольку в левой части отрезка запроса берется минимум от ai и расстояния до левой границы, а в правой — до правой, поделим отрезок пополам и будем считать каждую часть отдельно. Левая часть для запроса:
Вычтем из каждого слагаемого суммы $i$. Получим
Очевидно, что если мы умеем считать $ansLeft`$, то мы сосчитаем и ansLeft. Для того, чтобы его сосчитать, воспользуемся деревом отрезков, в вершинах которого хранится сумма и количество элементов на отрезке. Тогда, если у нас на отрезке лежат все элементы, меньшие - 2x + 1, то ответ равен их сумме плюс количество оставшихся (т.е. тех, которые больше либо равны - 2x + 1) умноженное на - 2x + 1. Поэтому просто будем класть запросы в порядке возрастания - 2x + 1 и находить сумму на отрезках.
"Правые" запросы обрабатываются аналогично, только вместо вычитания i надо делать прибавление.
Внезапно вспомнил о задаче C (сосульки) — что-то её так и не разобрали. Как решать?
Эгегей!
Я попробовал написать на контесте примерное следующее:
Отсортируем все шарики в порядке увеличения высоты, и будем рассматривать их в этом порядке: будем помечать каким-нибудь образом, что отрезок с x_i-r по x_i+r покрывается для каждого шарика. Если добавлять их с приоритетом, зависящим от высоты, то потом, пробегая по массиву длинной 10^7, который отвечает за сосульки, можно для каждой сосульки легко определить, какой именно шарик её убивает первым. Затем нужно взять первые (по времени) 10^5 событий вида сосулька убивает шарик и просто вычислить ответ по их значениям (просуммировав и поделив на количество).
Решение, на самом деле, не зашло(получило ва), но мне кажется, что из-за моей криворукости, а не из-за неправильности. Извиняюсь, если объяснение непонятное =)
Upd: Самый сложный шаг — определить для каждой сосульки, какой именно шарик её убивает первым. Для этого, добавим в массив два события для каждого шарика, соответствующие тому, что шарик начинается в данной координате и тому, что шарик заканчивается в данной координате.
Затем отсортируем все эти события и будем обрабатывать их слева направо, при этом храня set из всех ординат "текущих" шариков. Будем рассматривать соседние события и помечать все сосульки, соответствующие промежуточным точкам между двумя последовательными событиями тем шариком, что находится в вершине set'a. Всё остальное, вроде бы, должно быть понятно.
Идем слева направо и поддерживаем хип шариков по высоте центра. Тогда к текущей сосульке ближайший шарик — тот, что в топе хипа. Потом просто среднее арифмитическое по всем помершим сосулькам вывести
Ещё важно, что у всех целые координаты, поэтому вместо того, чтобы рассматривать сосульки как отрезки, можно просто посмотреть на две крайние точки у каждой сосульки.