→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
32:54:11
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
32:54:11
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 08:40:50 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











how to solve div1 250 ?
I solved it using this technique.
There will be some point such that you will not make moves crossing this point in your optimal solution. Therefore you can try all cyclic shifts, solve each of them as problem on array (where first and last elements aren't adjacent) and pick best result.
How to solve problem for array: result is equal to sum abs(pref_sum_A[i]-pref_sum_B[i]) over all i. Idea is following: it makes no sense to move some element in opposite directions (you can cancel such pair of moves), therefore if you have X elements in prefix of first array and Y elements in prefix of second array, there will be abs(X-Y) moves through the cut after this prefix — because you have to make X=Y, and you'll be either moving items from suffix into prefix or from prefix into suffix — but not both.
How to prove the first point? I can feel it intuitively, but dont know how to prove it.
This is probably one of those problems in which the organizers don't actually expect you to prove it (I hate submitting unproven solutions, so these kinds of problems crush me q.q)
Anyway, suppose the optimal solution crosses every point. Let's call a series of moves in a single direction a "segment", i.e. 1->2->3->4 is the segment 1->4.
Obviously moving stones in a full circle is not optimal because it doesn't change anything, so let's ignore that case. The final sequence of moves can then be represented by an even number of segments that reverse direction, for example 1->4, 4<-8, 8->12, 12<-1.
Consider the sums of the lengths of all odd and even segments. Without loss of generality, if the sum of all odd segments is larger than or equal to the length of all even segments, you can switch a stone from each odd segment to each even segment, giving you a solution that is just as good as the original one. Continue moving stones from odd segments to even segments until an odd segment has no more stones left, and you've created a solution that is also optimal and in which at least one point is never crossed.
any proof or intuition behind your logic ?
You can actually generalize this to get O(n) solution for the circular case too.
Without an extra log? I can solve it in and an author explained me
and an author explained me 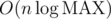 solution with ternary search. What about O(n)?
solution with ternary search. What about O(n)?
Without giving a lot of spoilers, if we're thinking about the same thing, you actually don't need to sort and add an extra log, as you only need one element (and nth_element is linear).
My practice room solution implements that idea if you're still confused.
Edit: Actually, look at the solution below, it's much nicer.
the origin of the problem is here, and O(n) average solution is described here
I tried to find pairs of piles such that one has a surplus and the other has a deficit of stones. I used a greedy approach (taking the adjacent piles first, then piles with distance 2 and so on ... ). Is this O(n^2) approach wrong?
Let X be the number of stones that passes through the border between 0 and 1 in 0->1 direction (if X is negative, it means that -X stones passes through the border in the opposite direction).
Then, X+a[1]-b[1] stones must pass through the border between 1 and 2 in 1->2 direction, X+a[1]-b[1]+a[2]-b[2] stones between 2->3, ... and so on.
Therefore the problem reduces to the following: find X that minimizes the sum |X| + |X+a[1]-b[1]| + |X+a[1]-b[1]+a[2]-b[2]| + ...
This is equivalent to a well-known problem where you are given points on a line and you need to find a point that minimizes the sum of distances to the given points. The solution is the median.
Any ideas on how to solve Div 2 1000 ?
http://ideone.com/LmPqxj — one but not so obvious DFS. In my code a variable
waysdenotes the number of subtrees with this vertex as the topmost vertex. And variableprefis the sum of sizes, needed for the answer. I process children one by one, always merging two first children into a new one. Merging two children a, b is as follows:I understand ways = ways[a] * ways[b] (to find the total subtrees), but I'm having trouble understanding why pref = ways[a] * pref[b] + ways[b] * pref[a] computes the total sum of sizes for the current node. Can you please elaborate?
One simple solution for Div1-Hard: the answer is 4^k * p(t) where p is a polynomial with degree is O(n+m). So we can get answers for k = 0, 1, ..., n+m by bruteforces, then get the answer for large k by Lagrange Interpolation. (Code: http://ideone.com/z1GXl8)
This solution is O(n^3) (assume n = m). In fact, the writer has an O(n^2) solution, but it looks very hard, so we reduced n to 100 to allow more solution to pass.
Is it easy to see that p is a polynomial?
I was a writer this time. cgy4ever did it in this way (just sketch):
Consider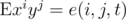 for 0 ≤ i ≤ n, 0 ≤ j ≤ m as function of t. Then e(t + 1) = Ae(t), where A is some matrix. It gives that e(t) obey some reccurence, one can prove it is polynomial from here.
for 0 ≤ i ≤ n, 0 ≤ j ≤ m as function of t. Then e(t + 1) = Ae(t), where A is some matrix. It gives that e(t) obey some reccurence, one can prove it is polynomial from here.
One not so simple solution for Div1-Hard: If you rotate by 45deg ((x,y) -> (s,t)=(x+y,x-y)) then the s-coord and t-coord move independently.
If you expand ri you'll notice that any term with an odd power for any ds will have expected value 0, otherwise it'll be 1, so we just need to count those. You can do that with a dp in O(n^2), state being i and how many of the ds currently have odd power. Overall the algo can be implemented in O(n^2).
Edit: Rip, i've reused the name t, I hope it's clear from the context which is which.
Actually with some more thought I've sped it up to O(nlgnlgt). Basically everything can be sped up with fft. We have
where the sum is over length t sequences a of non-negative even integers with sum j. r0, ... has generating function
r(x) = (x0 / 0! + x2 / 2! + ...)t
As we only need the first n+m terms of this we can just fast exponentiate using FFT in O(nlgnlgT) and then use r(x) to calculate E(ri)s. We can do similar FFTs to calculate E(si), E(ti)s from E(ri)s and then to calculate Ai, n + m - i s, which are the terms we need in our final sum (I left out that j = n+m-i in my first comment).
C++ Code
How did you obtain the generating function for rj?
It's not hard if you are good at mathematics!
How to solve Div1 500?
For every prime p count vp(a0), vp(a1), ..., vp(an), where vp(x) is the largest k such that pk divides x. Sort these arrays. Then for the first number take the product of the largest vp(ai) for all p, for the second — the product of the second largest vp(ai) for all p and so on. It's obvious that this answer is optimal and reachable from the initial array.
For each prime numbers its occurrences (after factorizing numbers) will be sorted by the exponent degree. Let's say that the input sequence is 25·38·51, 27·510, 23·34·54. Then, prime number 2 has its occurrences sorted as 27, 25, 23 and similarly for primes 3, 5. The final sequence should be 27·38·510, 25·34·54, 23·51.
That was the intended solution. But I was retarted as a tester and I came up with much harder solution only. I simulate the process, carefully choosing the order of operations. I can explain if anybody wants it. Code — http://ideone.com/BCOUcE
Wow, I came only to the harder solution during the SRM.
Thank you aid and Errichto for a nice explanation!
Does anyone know how to break mincost-flow solution in 250-d1? I made two unsuccessful hacks because of it. :(
The only finite edges are incident to either source or sink so there will be only n iterations of dijkstra. So it's O(n2log(n)), you can't break it.
My MCMF code got broken by a random large case. Same for some others in my room.
That's because you add O(n2) edges. You only need edges from source, to sink and between adjacent positions. Then you will have O(n) edges.
Ah, yes. Can you please explain your graph construction (capacities and costs for the edges)?
There are edges from the source to every position with zero cost and capacity max(a[i] - b[i], 0), edges from every position to the sink with zero cost and capacity max(b[i] - a[i], 0) and edges between adjacent positions with cost 1 and infinite capacity. I didn't write this solution because I thought that it would be an overkill. Instead I thought of another simpler solution but it turned out to be wrong.
Okay. I understand now. Thanks for your help. :)
How to solve Div 2 500?
I feel it is similar to GERGOVIA?
O(N^2) Greedy.
A solution only exists if the sum of both arrays are equal, if not output -1.
Start with an empty set {}.
Go from 1 to N, and at each step, solve for element number i. Maintain an invariant that all elements to your left have their target values ( all of them) so it makes no sense to change them, only look to the right.
Let curr[] denote initial configuration, and goal[] denote the desired configuration.
if curr[i] > initial[i]..You've excess, and since all elements to your left are with correct values, the excess must go to the right, you don't know where, but anyways, it has to move, so moving it to i + 1 does not make your answer worse.
if initial[i] > curr[i]..Keep moving to the right, and adding elements till initial[i] = curr[i]. ( This is not the two pointers method, after you fix i, you will start again from i + 1).
At step N, initial[N] must be equal curr[N] as you already fixed all values, and sums are equal.
Clearly if initial[i] = curr[i] do nothing.
Make sure to use long long when summing arrays.
Note: The above strategy does not work for Div1 250.
web statistics hasn't been updated yet, why?
Looks updated now