Всем привет!
Завтра в 19:00 MSK, состоится очередное соревнование по спортивному программированию Topcoder SRM 684.
Приглашаю всех к участию!
Предлагаю обсудить задачи после контеста.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Всем привет!
Завтра в 19:00 MSK, состоится очередное соревнование по спортивному программированию Topcoder SRM 684.
Приглашаю всех к участию!
Предлагаю обсудить задачи после контеста.
| Название |
|---|



Congrats with the new colour :-)
Thanks =)
Can we set hotkey for Batch Test in TC Arena?
It is ctrl+B or alt+B, I don't remember which one.
I would like to recall this comment :((
P/s: Could anyone give me an idea for Div.1 medium?
One may speed up the O(nk2) dynamic programming solution by noticing that at any stage of the DP the answer for x = p1α1·...·plαl depends only on the multiset of numbers (α1, ..., αl) and there's only about a hundred different multisets for k ≤ 50000.
UPD. For the n'th stage
The first term does not depend on b, the transitions in the second term depend only on the structure of the divisors of b so the numbers with equivalent structure can be grouped together to speed up the counting.
One may implement naive solution because of having no idea how to solve this problem, take a look at results of that solution, notice that dp[i][j] can be grouped — for all j such that K/j==X answer will be same. After that we can compress our numbers using square root trick (either j<=SQRT or K/j<=SQRT), build a DP graph with ~15000 edges on max.test and run naive dp, which now works in n*15000 instead of n*k and runs in 1.2 seconds on worst case.
Sound sad, I guess now I'll try to understand proper solution :)
Are you sure, that it is correct?
If you do the dp the other way around, you can get this.
I don't get it. For k = 100 do we have dp[2] = dp[97] for each "stage"? Because 2 is prime and 97 is prime?
Yes, if dp[k] means "number of sequences that start with number k".
got it
That's a really cool solution. Thanks!
doesn't it depend on multiple of b?
Denote zn correct sequences. zn = kn - wn, where wn for incorrect sequences.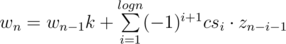 , where csi is the number of sequences of length i + 1 that each pair of adjacent values is bad (so x, x·k1, x·k1·k2, ..., x·k1... ki). The last thing can't have the size more than logn, so it can be calculated by simple dp.
, where csi is the number of sequences of length i + 1 that each pair of adjacent values is bad (so x, x·k1, x·k1·k2, ..., x·k1... ki). The last thing can't have the size more than logn, so it can be calculated by simple dp.
I used the same idea and got better asymptotics. I made divide and conquer: let's denote f(n) -- the answer for the problem. let's denote n1 = [n/2], n2 = n — n1. Then f(n) = f(n1) * f(n2) — F(n1-1,n2-1,1), where F(n1, n2, len) = the number of sequences of length n1 + n2 + len + 1 such that the first n1 and last n2 -- are good subsequences (without subsequent kx,x) and there is a subsequence in the middle of length len + 1 of such of a pattern: k1*k2..*klen*right, k2*k3*..*klen*right,..,right. len <= log(n) so that middle sequence can't be too long. How to count F(n1,n2,len)? F[n1][n2][len] = f(n1) * dp[len] * f(n2) — F(n1-1,n2,len+1)-F(n1,n2-1,len+1)-F(n1-1,n2-1,len+2), where dp[len] is the number of dividing sequences with length of len + 1 (which we put in the middle). We can count dp[len] easily in len*nlogn (it's precalc), but the main part works in no more than log*4 * log * log (we will count only 4 * log * log f(k), the last log is for set, we can change it to O(1) with Hashmap). So it's really fast.
I was a bit disappointed when heard about the updated square solution.)
Nice! Anyway the worst part of my solution is the same precalc with O(nlog2n) complexity, so they have the same complexity :-)
I also can't understand why the constraints are so small.
So that the other solution could pass, too? It's something like n·x2 divided by some small constant, where x is the number of different classes of integers from 1 to k. Perhaps it can be improved to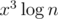 if we utilize matrix exponentiation, but that's more work.
if we utilize matrix exponentiation, but that's more work.
My solution reports x = 132 for k = 50 000. When I tested it repeatedly in the last minute of coding phase, it took 1.6 to 2.2 seconds to run on max-test (
calcsays n·x2 is 871 200 000), I'm really lucky it passed system tests. Of course, it can be optimized by avoiding iteration overmap <int, int>in the inner loop, I just had no time left in the coding phase.Yes, it can be improved using matrix exponentiation to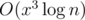 , because all of the transitions are linear. cgy4ever was fully aware of this, as he commented something to this effect in the chat after the match.
, because all of the transitions are linear. cgy4ever was fully aware of this, as he commented something to this effect in the chat after the match.
I fully agree with not forcing people with the main insights figured out to code matrix multiplication on top of the whole compression and whatnot they already had to do, keeping in mind TC SRMs are only 75 minutes long.
Gassa, do you mean that iterating over
mapis slow? I thought it's O(n) and iterating overlistorvectorwouldn't be faster. Or would it be?And regarding the question about constraints. My solution is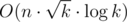 I think. I had x = 446 groups, link to code.
I think. I had x = 446 groups, link to code.
Iterating over a map is O(n), but the constant factor would surely be less with an array of pairs.
I've checked in the practice room. My original solution passed in 1.95 seconds — pretty dangerous! Transforming the map into a simple array of pairs brings it down to 1.6 seconds — a 20% speedup, I hoped for more. Optimizing the number of
MODoperations gets the solution to run for 1.25 seconds — another 20%.Of course, the Right Way (TM) is to measure before you optimize, but at the end of a contest, one sometimes has to resort to guesses.
many challenges, how so?
Overflows in the first problem (my solution also was challenged with overflows).
In Div1 Easy, there were also solutions which assumed the answer is always a consecutive segment in the sorted array. Such solution passes all examples.
In Div1 Easy there were also solutions with assumption that the answer starts with two consecutive elements in the sorted array.
Counterexample: 1 2 3 5 7 9 and k = 4 (answer is 1 3 5 7 9).
Div 1 medium?
And if anyone could help me look at this code that would be awesome. I tried using matrix exponentation on a linear recurrence, relearnt it over the competition and submitted 15 seconds before haha, but got hacked. If anyone could give me a hint as to where I went wrong that would be awesome :).
https://gist.github.com/anonymous/3817f7de6696dc354763
isn't it O(k3)?
Yeah maybe that's the problem.
I was so proud I figured that out, wrote a what seems to be correct solution (but probably too slow) as it passed examples and relearnt matrix exponentation within the time though haha.
Well I guess O(k^3) is the problem yeah. Thanks.
I think memory is O(k * k) so if k is reasonably large for example : k = 50000, memory usage is more that 256 MB
Any hints for div1 250? :|
First note that for an array to be k-smooth it has to satisfy that the minimum value of the array times k is bigger than or equal to the maximum value. In the case of the problem that min and max is substituted by min and max differences.
I solved it by first sorting the array and then considering all pairs (i, j) where j > i, choosing these as the maximum and minimum, the max difference since it's sorted is now a[j]-a[i]. Now we can greedily choose which elements in the range that we can include in our set, start from i find the first value (let's say it's at position p) iterating towards j that satisfies that (a[p]-a[i])*k >= a[j]-a[i], you know as soon as you reach this that all elements beyond it will also satisfy this because the array is sorted. Then make your new anchor this point and keep iterating forwards until you hit the end.
The proof for the greedy method is something along the lines of it's always better picking the first one because picking a later one would make at least as many values in front of it invalid to pick because the array is sorted.
Any questions to my explanation?
Great Explanation, thanks!
Here is a generally straightforward solution: let's fix smallest difference in our set (n^2 ways) and smallest element (n ways). Now we can implement n^2 DP — what is maximum size of valid subset with largest element being equal to x; you have n states and n transitions from each state (trying new largest element and checking that it's not too small when compared to last element in our set and not too large when compared to smallest element). Resulting complexity will be O(N^5). Not the best one, but at least it is clearly correct and you don't need to prove any assumptions/greedy ideas.
Misunderstood the solution.
In the first step I'm fixing only smallest difference between two adjacent elements, how can I figure out smallest element from it? I can make some pruning here, like not trying smallest elements which are larger than elements involved in smallest difference, but how can I figure out smallest element itself?
Sorry, there's been a misunderstanding somewhere.
I meant, one can loop on every pair of actual elements in the list instead of looping on the possible values of the differences. Then do O(N^2) DP. Yielding O(N^4).
Does that make sense?
Edit: Petr's solution seems to do that by looping on the maximum difference first then doing DP to find the maximum subset while satisfying the minimum difference constraint.
Hmm, the title of the problem (CliqueParty) misled me into thinking it's a graph problem. I actually "reduced" it to trying to find the minimum nodes to remove so that all the edges would disappear (an edge would mean that the two numbers cannot be in the final set together). I couldn't find a good algorithm for this, though.
I guess setters don't hide hints in problem names.
I think that would be Minimum Vertex Cover which is NP-Hard :)
I checked if the graph is actually a tree, so that the minimum vertex cover can be solved greedily. But it is clearly not a tree.
I don't submit easy without proving last SRM, I fail, I submit without proving this SRM, I fail again
Div1 Easy > Div1 Medium confirmed
Solved difficult medium and failed easy. Two fails (also CF345) in a one day :-(
High five o/, I failed cf345 too because I ignored clarification for B and spent too much time debugging...
I was expecting to become orange today anyway because of the 6am starting time, but I can't justify not taking part in a fun contest just to hold a color.
I understand the problem B wrong: I thought we can skip some images. I've wrote the solution (I'm not sure, but it seems it is correct) and only after that realized that the problem is much easier.
can someone please explain how to solve div. 2 600 and 900 points questions?
d2 600: come up with a dp solution dp[i][j] = number of sequences of length i ending with the number j. Then, you can write a recurrence like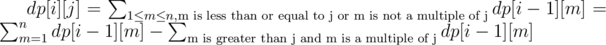 . Naively, this seems like O(nk^2), but see if you show there is someway to do it in O(nk*logk) instead.
. Naively, this seems like O(nk^2), but see if you show there is someway to do it in O(nk*logk) instead.
d2 900: The first thing that should come to mind is that this is a graph problem. Let's suppose the graph had no cycles. Then, you have this problem: http://stackoverflow.com/questions/16124844/algorithm-for-finding-a-hamilton-path-in-a-dag So, how do we deal with cycles? We compute the condensation of the graph, then apply the algorithm in the link. Easier to code solution (but harder to prove): You can show these 2 conditions are necessary and sufficient. Every node is reachable from node 0. For each pair of nodes x,y, either there is a path from x to y or a path from y to x. So, another solution is to return no if either of those two conditions is violated, otherwise return yes.
Does anyone have any idea hot to solve div1 hard?
Try to look at it combinatorially. As an intermediate step, try to show that the sum of m! / (s[1] * s[2] * ... * s[n]) over all permutations is equal to m! / (x[1] * x[2] * ... * x[n]). I can post a more detailed solution later if you're still stuck.
I saw Petr's proof of that fact in the arena chat, but I still can't solve the remaining combinatorial problem in a good enough complexity, so I'd love to see the whole solution :)
My model differs from the one that Petr described in the arena (he described something with cycles in a permutation).
Here is my model: Suppose we have m balls with n colors, where there are x[i] balls of the i-th color, labeled from 1 to a[i]. We will show that the sum is equivalent to counting the number of ways of arranging the balls in a line such that the first occurrence of a color is the ball with label 1 for all colors. The number of ways can be computed with probabilities, in that each color is independent and has a 1/x[i] chance of having the ball with label 1 being first. For the sum, let's fix a permutation of the colors. Among m balls, the probability the first ball has color p[1] and label 1 is 1/s[n], the probability the second ball has color p[2] and label 1 is 1/s[n-1], and so on. So, this particular permutation contributes m!/(s[1]*s[2]*...*s[n]) to the sum. Thus, this shows the sum over all permutations is m!/(x[1]*...*x[n]).
To deal with the missing s[1], this means that the color that appears last does not have the constraint that it needs to have a ball with label 1 as the first occurrence. To count this, we fix the ball which is the last color that shows up. Then, we need to arrange the remaining balls so that the first occurrence of those colors comes before the first occurrence of the last color. So, this gives a dp solution based on how many balls are to the right of the first occurrence of a ball of the last color. You can see my code here (http://pastebin.com/KegwgXdp) to fill in the remaining details. The runtime is O(n^3*m). There are probably other solutions that are faster.
Another solution. In this explanation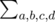 means that the sum is taken over all permutations of {a, b, c, d}.
means that the sum is taken over all permutations of {a, b, c, d}.
It is easy to verify that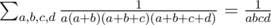 . However, in this task we want to compute something like
. However, in this task we want to compute something like  .
.
Since it's difficult to handle high-degree polynomials of X in denominators, rewrite it as follows:
Let's take a close look at the first term:
Other terms can be simplified similarly, and we get the following formula:
where sum(S) denotes the sum of all elements of S.
Now the remaining part is straightforward. Fix the first element of the permutation and write it as X. a, b, c, d correspond to other elements. Compute the distribution of sum(S) and the parity of S using a simple DP. Compute the answer using the formula above.
But how to come up with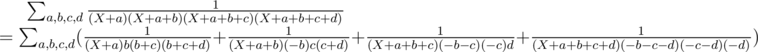 ? I can prove it using Lagrange polynomial but how to invent it from scratch?
? I can prove it using Lagrange polynomial but how to invent it from scratch?
Let's find c1, c2, c3 that satisfies
We can compute these values by solving a system of linear equations of three variables, and turns out that
Then we can guess the general formula. Verify the following using Wolfram Alpha:
Yay, editorials are now available here.