Приветствую всех участников раунда!

Давайте проведем разбор задач в примерном порядке их сложности

182B - Vasya's Calendar

Обратим внимание, что Вася должен вручную прибавлять номер дня только тогда, когда заканчивается один месяц, и начинается следующий. Значит, пусть у нас в текущем месяце было x дней, а в следующем уже y. Тогда в первый день следующего месяца часы будут показывать день x + 1 (не забываем про модуль d), а должен показывать номер 1.

Очевидно, что Вася должен вручную прибавить d - x дней, чтобы часы показывали то, что нужно.

Значит, ответ — это сумма всех чисел d - a_i, где 1 ≤ i < n.

182D - Common Divisors

Эта задача решается многими способами, но самый простой подход следующий: найдем все делители строки s₁, все делители s₂ и найдем пересечение этих двух множеств.

Как же найти все делители строки? Пусть t — это делитель строки s. Тогда очевидно, что |s| = 0(mod|t|), а также t является префиксом строки s. Эти соображения и позволяют найти все делители строки, а именно переберем длину префикса, проверим делимость, а потом проверим, что префикс записанный подряд нужное количество раз совпадает с s.

Всего подходящих префиксов не более 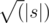, проверка каждого работает за O(|s|), значит, итоговое решение за 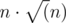, где n = max(|s|, |t|).

Найти пересечение двух множеств строк несложно, можно воспользоваться стандартными структурами данных

182E - Wooden Fence

Условие задачи было сформулировано неверно, что привело к несоответствию решений, правильный вариант условия появится совсем скоро, приносим участникам свои извинения.

Основа решения этой задачи — это динамическое программирование.

Состояние — (last, type, l), где last — номер последней доски, type характеризует поворот последней доски, а l — длина оставшейся части забора.

Пересчитывать эту динамику тоже очень просто: переберем номер следующей доски, ее поворот, проверим подходит ли она в текущее состояние, и прибавим нужную величину.

Асимпотика решения — O(n²·len).

182C - Optimal Sum

Представим мысленно задачу в виде движения слева направо некоторого окошка длины len по исходному массиву. То есть нам нужно найти способ достичь максимума в выбранном окошке, а потом сместить его на одну ячейку вправо.

Пусть мы зафиксировали положения окошка, теперь посчитаем ответ. Для этого отдельно запишем все положительные и все отрицательные числа в окошке. Если положительных не больше, чем k, или отрицательных не больше k, то мы можем все числа сделать одинакового знака, и ответ — это сумма модулей чисел в подмассиве. Это простой случай.

Несложно понять, что невыгодно некоторые отрицательные числа делать положительными и одновременно некоторые положительные — отрицательными. То есть мы обязательно выберем знак <<+>> или <<->> и k чисел этого знака сделаем противоположными. Также несложно понять, что всегда при смене знака у некоторых чисел выгодно брать ровно k максимальных по модулю чисел этого знака.

Для того, чтобы поддерживать движение окошка будем использовать два отдельных дерева отрезков: одно для отрицательных, другое для положительных чисел.

Если в вершине дерева хранить пару (количество чисел в поддереве, сумма этих чисел), то такая структура умеет возвращать сумму k максимальных чисел, что нам и требуется.

Асимптотика решения — O(n·log(n)).

182A - Battlefield

В этой задаче есть два главных момента:

1. длина любой траншеи в метрах численно не превосходит b

2. траншеи не пересекаются

Первый пункт означает, что если Вася забегает в траншею чтобы переждать, пока лазер работает, то за это время он может придти в любую его точку.

Второй пункт означает, что пока лазер работает, Вася обязан находиться в той траншее, в которой он на данный момент сидит.

Значит, путь Васи — это перебежки от одной траншеи к другой, где он пережидает лазерную атаку. Таким образом все решение задачи — это найти кратчайший по времени путь по траншеям от стартовой точки до конечной (их мы тоже будем считать траншеями, просто нулевой длины), для этого нужно всего лишь предподсчитать матрицу расстояний между отрезками траншей и запустить алгоритм, например, Дейкстры.

Два тонких момента:

1. мы не можем перебегать между траншеями, если между ними расстояние больше a

2. пусть Вася прибежал в момент времени t, теперь нам нужно найти момент, когда он сможет убежать дальше. Для этого нужно найти следующий момент времени, когда лазер будет перезаряжаться. Эта величина T несложно ищется по формуле:

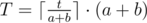
Асимптотика решения — O(n²).