Shuaib's blog

Sum of digits of factorial problem
By Shuaib, history, 9 years ago, In English

Hi,

How can I find the sum of digits in a factorial of a number N, where N can be in range [1, 2000]? Can it be done without resorting to BigNum libraries?

  • Vote: I like it
  • -2
  • Vote: I do not like it

Comments Comments (8)
| Write comment?
»
9 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Think of logarithms.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you please elaborate. I am looking for a Log(N) complexity. The algorithm given below by sbakic uses string multiplication, which won't be Log(N).

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 5   Vote: I like it 0 Vote: I do not like it

      -deleted-

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 4   Vote: I like it +5 Vote: I do not like it

        Why did you delete your answer? I think it can actually work: if we know the number D of digits of the factorial F = N! and its log L = log(F), we can do some binary search in the factorial digits since log(x) is unique. For example, to find the most significant digit of the factorial we will try every 0 ≤ i ≤ 9; when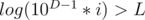 we know that the most significant digit is i - 1. After that, we store the "current log" and do it again for the second most significant digit and for the third and so on... Overall complexity would be .

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      → Reply
»
9 years ago, # |
  Vote: I like it -7 Vote: I do not like it

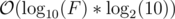This is the algorithm for factorial of a number. Next step is trivial.

#include <iostream>
 
using namespace std;
 
string multy(string a, string b) {
  int n = a.size(), m = b.size();
  int array[n + m];
  for (int i = 0; i < n + m; i++) {
    array[i] = 0;
  }
  for (int i = n - 1; i >= 0; i--) {
    for (int j = m - 1; j >= 0; j--) {
      array[i + j + 1] += (a[i] - '0') * (b[j] - '0');
    }
  }
  for (int i = n + m - 1; i >= 0; i--) {
    array[i - 1] += array[i] / 10;
    array[i] %= 10;
  }
  string s = "";
  for (int i = 0; i < n + m; i++) {
    s += array[i] + '0';
  }
  s.erase(0, min(s.find_first_not_of('0'), s.size() - 1));
  return s;
}
 
string power(int n) {
  string s = "1";
  int t = n;
  for (int i = 0; i < n; i++) {
    s = multy(s, to_string(t--));
  }
  return s;
}
 
int main(){
  int n;
  cin >> n;
  cout << power(n) << '\n';
  return 0;
}
→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

Can you give problem link, please?

→ Reply