Разбор задач будет пополняться :)

Разбор задачи <<Развивающая игра>>

Это была самая простая задача из сложного набора. Для начала заметим, что можно решать данную задачу для каждого элемента a_i отдельно. То есть, если мы фиксируем некоторое k, то вклад каждого a_i в ответ можно считать отдельно.

Итак, фиксируем некоторое a_i. Найдем максимально возможное j такое, что i + 2^j ≤ n. Несложно видеть, что для всех k < i + 2^j вклад a_i в ответ будет равен a_i. То есть нужно будет сделать a_i ходов с переходом в a_i + 2^j. Далее найдем такое максимальное u, что 2^j + 2^u ≤ n. Заметим, что u < j. Также заметим, что для всех k таких, что i + 2^j ≤ k < i + 2^j + 2^u вклад a_i в ответ будет равен 2·a_i. Далее найдем такое q, что i + 2^j + 2^u + 2^q ≤ n.

Итак, для каждого элемента a_i мы должны найти соответствующую последовательность степеней двойки. Очевидно, что общая сложность этого процесса .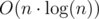

Теперь нам нужно считать ответ. Можно это делать, например, так: будем хранить массив b_i. b_i — это изменение ответа при переходе от i к i + 1. Этот массив строится тривиальным образом во время построения последовательностей степеней двоек. И потом по нему также нетрудно получить ответ. Итого, сложность решения составляет .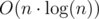

Разбор задачи “Жадные торговцы”

Для начала заметим, что торговцы будут платить только за те ребра, которые являются мостами (мостами называются рёбра неориентированного графа, при удалении которых количество компонент связности в графе увеличивается). Все другие ребра не подходят, так как при их удалении граф останется связным и путь между никакими двумя вершинами не исчезнет. Итак, первым этапом в решении является поиск мостов. Воспользуемся для этого известным алгоритмом, который работает за время O(n + m).

Далее заметим, что при удалении всех мостов граф разбивается на несколько компонент связности (возможно, одну). Построим новый граф, в котором полученные компоненты будут вершинами, а мосты исходного графа -- ребрами. Заметим, что этот граф является деревом. Его связность следует из того, что исходный граф связный, а отсутствие циклов в нём из того, что ребра в нём соответствуют мостам в исходном графе.

Заметим также, что число динариев, которое заплатит каждый из торговцев — это расстояние между некоторыми двумя вершинами в новом графе. Но так как этот граф является деревом, эти расстояния можно искать быстро, используя алгоритмы поиска LCA (наименьшего общего предка) для двух вершин. В данной задаче можно использовать один из самых простых алгоритмов поиска LCA, который осуществляет препроцессинг за время 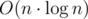и обрабатывает один запрос за . Сложность такого решения составляет .

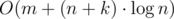Отметим также, что решение можно несколько упростить. Построим дерево рекурсивного обхода исходного графа и назначим веса его ребрам. Вес, равный 1, будут иметь мосты, а все остальные ребра будут иметь вес, равный 0. Тогда после этих преобразований для нахождения ответа для одного торговца достаточно посчитать расстояние между двумя вершинами в построенном дереве рекурсивного обхода.

Разбор задачи <<Бобер и разрешение коллизий>>

Заметим, что при обходе ячеек с шагом m по модулю h множество ячеек хеш-таблицы разбивается на некоторое количество циклов, в каждом из которых одинаковое число элементов. При этом число циклов равно НОД(h, m), а число элементов в каждом из циклов -- h / НОД(h, m). Смысл циклов в том, что если объект имеет изначальное значение хэш-функции внутри одного цикла, то он будет добавлен в качестве элемента этого же цикла.

Теперь можно работать с каждым циклом отдельно. Нам необходимо эффективно добавлять/удалять элементы и при этом считать число коллизий. Для этого проще всего использовать для каждого цикла дерево отрезков или комбинацию из бинарного поиска и дерева Фенвика.

Cложность такого решения составляет 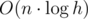для дерева отрезков или 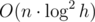для бинарного поиска и дерева Фенвика. Заметим, что большой разницы в скорости работы этих решений нет за счет скрытых констант при подсчете сложности.

Разбор задачи <<Магические квадраты>>

Рассмотрим два подхода к решению данной задачи. Заметим, что для начала мы по исходным данным определяем значение s как сумму всех чисел, делённую на n. Далее будем пользоваться этим значением при решении.

Первый подход – переборный. Он основан на двух идеях:

• Можно в процессе перебора однозначно определять числа в некоторых квадратах. Например, если мы выбрали значения трех элементов главной диагонали, то выбор четвертого однозначен. Таким образом, мы сокращаем число вариантов в переборе.
• При поворотах и отражениях магический квадрат остается магическим квадратом. Если реализовать эти идеи аккуратно, то можно было решить данную задачу.

Второй подход основан на дискретной оптимизации. Рассмотрим следующий функционал качества: Q = |sum₁ - s| + ... + |sum_t - s|, где |x| — абсолютная величина x, t = 2 * n + 2, sum₁, .., sum_n — суммы в строках квадрата, sum_n + 1, sum_2n — суммы в столбцах, sum_t - 1 — сумма элементов на главной диагонали, sum_t - 1 — сумма элементов на побочной диагонали. Итак, мы должны найти такую перестановку, которая минимизирует данный функционал. Можно это делать так: выберем случайную перестановку. Будем пытаться делать в ней инверсии, которые улучшают исходный функционал качества, 1000 раз. Если в итоге Q = 0 — мы нашли ответ, если Q > 0 -- возьмём другую перестановку и начнём сначала. Даже такой тривиальный алгоритм оптимизации в данной задаче работает хорошо и проходит все тесты с большим запасом по времени.

Разбор задачи <<Задача от бобра — 2>>

Решение данной задачи можно разделить на две части:

• Удаление шума на изображении;
• Классификация фигур.

Для удаления шума можно было воспользоваться следующими методами:

a. Делаем следующие операции: сканируем изображение и по нему строим новое. Если некоторый черный пиксель имеет белых соседей, то мы его делаем белым. За несколько таких проходов мы избавляемся от почти всего шума на фоне. Потом делаем обратную операцию по замене былых пикселей на черные. Таким образом мы избавляется от шума внутри фигур.

Заметим, что после всех таких операций может остаться шум (в виде маленьких компонент черного цвета) и некоторые фигуры могут утратить связность. Обе эти проблемы решаются несложно: удаляем маленькие компоненты черного цвета и потом объединяем близкие компоненты черного цвета.

b. Можно было поступить проще. Выделяем компоненты черного цвета и отбрасываем те, которые имеют малый размер. Если внимательно посмотреть на тесты, то в реальности при равномерном распределении шума не возникает больших шумовых компонент черного и не теряется связность фигур. Однако предыдущий подход является существенно более надежным.

Самый простой способ для классификации фигур — это сравнение распределений расстояний от всех пикселей фигуры до центра каждой из фигур. Центр можно вычислить как среднее арифметическое координат всех точек фигуры. Сравнивать у распределений можно выборочные мат. ожидания и дисперсии.

Задача <<Репрезентативная выборка>>

Сразу приступим к полному решению задачи. Давайте отсортируем строки лексикографически и посчитаем lcp[i] -- длину наибольшего общего префикса строк i и i + 1. Несложно доказать, что наибольший общий префикс любых двух строк i и j теперь равен min (lcp[i], lcp[i + 1], ..., lcp[j - 1]) (подобное утверждение используется при использовании суффиксного массива). Это полезно.

Теперь применим метод динамического программирования. Сделаем такое ДП: F(i, j, k) — максимальный возможный ответ на задачу, если из строк с номерами i... j нужно выбрать ровно k строк. Переход следующий: найдём позицию p на отрезке i... j - 1 с минимальным lcp[p], тогда F(i, j, k) = max_{q = 0... k}(F(i, p, q) + F(p + 1, j, k - q) + q·(k - q)·lcp[p]), то есть предполагаем, что выбрано q из строк из i... p, k - q строк из p + 1... j, и для всех пар этих строк длина наибольшего общего префикса равна lcp[p] (это следует из утверждения в первом абзаце).

Такое решение достаточно для получения 50 баллов. Пока что кажется, что сложность этого решения порядка O(N⁴). Осталось показать, что на самом деле можно реализовать это решение так, чтобы его сложность оказалась равна O(N²).

Для начала заметим, что различных отрезков i... j, на которых нас интересуют значения функции F, на самом деле ровно 2N - 1, а не O(N²). Почему это так, можно понять из переходов нашего ДП. Отрезок 1... N разбивается на два отрезка 1... p и p + 1... N, каждый из этих отрезков разбивается ещё на два отрезка, и так далее; видим, что между позициями i и i + 1 для любого i ровно один раз за весь подсчёт ДП произойдёт <<разрез>>, и этот разрез породит два новых отрезка, на которых нас интересуют значения ДП. Отсюда и получаем оценку в 2N - 1 нужных отрезков, следовательно, наше решение уже имеет сложность не более O(N³).

Последнее и самое сложное — догадаться, что решение выше может иметь сложность O(N²). Например, реализовать его можно так. Давайте заведём рекурсивную функцию F(i, j), возвращающую массив длины j - i + 2 — собственно значения ДП F(i, j, k) (понятно, что нас интересуют только значения k из отрезка от 0 до j - i + 1). Внутри этой функции делаем следующее: найдём p, вызовем F(i, p) и F(p + 1, j), теперь переберём x от 0 до p - i + 1, переберём y от 0 до j - p и обновим значение F(i, j, x + y), если оно улучшилось (подробнее можно увидеть в авторском решении, там всё довольно прозрачно). Максимальное время работы функции F, вызванной на отрезке i... j длины j - i + 1 = N, можно записать как T(N) = max_{X = 1..N - 1}(T(X) + T(N - X) + (X + 1)·(N - X + 1)). Осталось понять, что T(N) = O(N²). Это можно сделать, например, написав простое ДП для подсчёта T. Если подумать, то можно понять это так: когда мы в цикле перебираем x = 0... p - i + 1 и y = 0... j - p, давайте будем представлять, что мы перебираем как будто пару строк: x = i... p и y = p + 1... j (тут перебор по x и y проходит на одну итерацию меньше, но это не принципиально); тогда каждая пара строк за весь подсчёт ДП окажется перебрана ровно один раз, что и даёт нам итоговую сложность O(N²).

Вот здесь можно ознакомиться с авторским решением.

Многие участники сдавали решения, использующее бор. Такие решения также могут иметь сложность O(N²), однако работают дольше и используют намного больше памяти. Тем не менее, ограничения по времени и по памяти были достаточно лояльны к разным решениям :)