Hi everyone!
For three years ABBYY Cup finalists have been meeting for ABBYY Open Day at the ABBYY Moscow office (Headquarters) in summer. This year hasn’t been an exception. As an organizer I will tell you about ABBYY Open Day 2013 which took place on July 17th.
 It should be noted that it was rainy all the days before the contest day. We were very concerned: we have announced the entertainment which was strongly depending on the weather. Evidently the Universe wanted to see the outdoor part of the Open Day and decided not to spoil the weather by rain. The day began with breakfast and watching a funny video with a promising name “The truth about ABBYY”.
It should be noted that it was rainy all the days before the contest day. We were very concerned: we have announced the entertainment which was strongly depending on the weather. Evidently the Universe wanted to see the outdoor part of the Open Day and decided not to spoil the weather by rain. The day began with breakfast and watching a funny video with a promising name “The truth about ABBYY”.
At 10:40 AM the contest started. For me as an organizer this is nice time. There is silence in the room, participants solve problems, I can relax for a moment watching the results and rooting for my favorites. In two hours we got the final standings. In particular, I want to congratulate with great results Mimino, who was the only non-speaking Russian participant. Every ABBYY Open Day cannot take place without the talk about the company. So, after dinner the participants met the CEO of ABBYY Sergey Andreev. Then our technical consultant for Compreno products Alexander Kostuchenko demonstrated achievements of ABBYY R&D in computer linguistics.

We’ve had a tour on the office where the participants managed to see how the working process of programmers is organized. At the end of the official part we’ve had the most pleasant event, the awarding. This year all the winners could get the gift from Smart Beaver himself, the main character of all ABBYY Cup problems. Next the unofficial part of the day began. It was the quest in the centre of Moscow. All the participants divided in teams, got the rules and the tasks and scattered throughout Moscow. In order to find the finish line the teams should have answered all the questions about Moscow sights or they could drop the quest at any time by calling us. However, nobody wanted to give up. Imagine how hard these tasks were for Mimino. We translated the rules especially for him and provided a translator to his team.
At 10 PM the teams started to gather at the finish in one of the Moscow’s anticafe. We have been waiting for them with pizza, salads and Smart Beaver! Our ABBYY Open Day has ended. We are very happy that there are participants who visit us every year. And this year we have had one international participant. It was nice to meet everyone. See you next year!
https://get.google.com/albumarchive/pwa/114842746780416406882/JInSLJ?authkey=Gv1sRgCLPuzoHEm4X_YQ









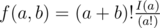 , where
, where 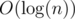 values if
values if 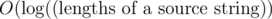 .
.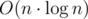 and handle one request for
and handle one request for  . The complexity of computations id
. The complexity of computations id 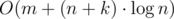 .
.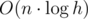 , of solution with Fenwick tree —
, of solution with Fenwick tree — 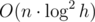 .
.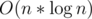 or
or 
