this is the problem link ...... http://lightoj.com:81/volume/problem/1097 it can be solved using bit but how does it fit into the complexity ??
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 154 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/22/2025 07:35:49 (l2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










The example helps us see that the answer is at most 1429431. Now we can easily simulate the process with the help of Fenwick tree or some other tree-like data structure but I prefer Fenwick when it's possible to use it since it's really really easy to code. So, let's say that all numbers are available at the beginning (increase all indices from 1 to 1429431 by 1). We should extend our data structure so that it can quickly tell us which is the K-th available number for given K. This can be easily done with binary search over the answer and then with the standard query we check if there are at least K-1 numbers less than the fixed. Also, every number is crossed out at most one time so our solution is actually fast enough — http://ideone.com/WmKP2d.
Implementation might be easier in this approach, but better complexity can be achieved with a segment tree based algorithm. To find the K-th available number you are doing a binary search with a Fenwick tree query. That's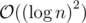 , while you can do it with segment tree in
, while you can do it with segment tree in 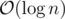 .
.
The idea is to store the summation of range in every node of the segment tree. Then if
k<=tree[left]then the answer is in the left child of this node. Otherwise, you need to look fork-tree[left]in the right side of the tree.BTW, why do you define common variables to gibberish? Are there any advantages? :p
Yes, I know that and an algorithm with slightly better complexity can be achieved with BST since its operations are O(log Size) instead of O(log MaxSize) which sounds better but I am pretty sure segment tree will perform better in practice and still I prefer the shortest working algorithm. And I saw such defines in I_love_Tanya_Romanova's codes and the first time I wondered wtf he was doing but some days after that I tried to declare a global variable called left and the compiler didn't allow me to do so because of some function called left which I didn't know it exists so that helps to avoid collisions :)
UPD: I forgot to put log in the brackets :D