Спасибо всем участникам нашего соревнования за множество успешных посылок по задачам!

Этот комплект для вас подготовили: snarknews, Chmel_Tolstiy, Gassa, Zlobober. Разбор для вас подготовили snarknews и Gassa.

Задача А. Буквы адреса

Поскольку множества гласных и согласных не пересекаются, при лексикографическом сравнении раньше будет та последовательность, которая начинается с буквы, которая раньше идёт в алфавите. Так что просто идём по строке, запоминаем первую гласную и первую согласную, которая нам встретилась. Как только встретились обе, сравниваем и немедленно выдаём ответ. Необходимо не забыть про случай, когда одна из строк пустая.

Задача B. Байтландский талер

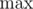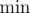Считываем первый обменный курс, инициализируем считанным значением переменные и . Затем в цикле считываем N - 1 оставшихся курсов. Если курс больше 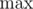, присваиваем считанное значение переменной 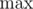, если курс меньше 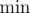— переменной .

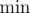Ответ равен .

Задача C. Шашматы

Так как чёрная шашка каждый ход уменьшает номер горизонтали, то всего шашка может сделать не более 7 ходов, на каждом ходу у неё не более двух вариантов выбора. Соответственно, конь тоже может сделать не более 7 ходов (даже если конь ходит первым, то, если шашка сделала 7 ходов, она дошла до первой горизонтали и игра заканчивается победой чёрных, то есть восьмого хода коня не происходит). Итого получаем не более 2⁷·8⁷ = 2²⁸ вариантов.

Все эти варианты можно за отведённое время перебрать рекурсивно. Для этого реализуем две функции:

• функция хода шашки, которая проверяет условия выигрыша/проигрыша на данном ходу (то есть что шашка достигает после этого хода первой горизонтали, берёт коня или же оказывается "запертой"), если ни одно из этих условий не выполнено, то вызывается функция хода коня для всех возможных вариантов хода шашки;

• функция хода коня, которая проверяет условия выигрыша на данном ходу (то есть что конь может взять шашку), если соответствующее условие не выполнено, вызывается функция хода шашки для всех возможных ходов коня (которых не более восьми).

В основной функции считываются данные и в зависимости от того, кто ходит первым, вызывается функция хода коня или функция хода шашки.

Задача D. Город в пустыне

Рассмотрим диагональ выпуклого пятиугольника. Одна из вершин лежит по одну сторону этой диагонали, две по другую и две лежат на этой диагонали. Первая вершина, соединённая диагоналями с двумя вторыми, даёт две точки пересечения, лежащие на выбранной диагонали. Остальные четыре вершины образуют выпуклый четырёхугольник, одной из сторон которого является исходная диагональ. Соответственно, точки пересечения остальных диагоналей пятиугольника (это точка пересечения диагоналей четырёхугольника и точки пересечения отрезков, соединяющих точки на одной из сторон с вершинами, с диагоналями четырёхугольника) лежат внутри четырёхугольника. Получаем, что точки пересечения диагоналей, не лежащие на данной диагонали, находятся от неё с одной стороны. Тем самым точки пересечения диагоналей выпуклого пятиугольника должны быть вершинами некоторого выпуклого пятиугольника D (сторонами которого являются отрезки диагоналей).

В этом случае исходные вершины восстанавливаются как точки пересечения прямых, содержащих несмежные стороны пятиугольника D. При этом точка пересечения каждой пары сторон должна существовать (то есть стороны не должны быть параллельны) и лежать по разные стороны с вершинами пятиугольника D относительно прямой, которая соединяет вершины сторон соответствующей пары (это следует из выпуклости исходного пятиугольника). Легко увидеть, что, если все эти требования выполняются, то восстановленный пятиугольник является выпуклым.

Тем самым решение состоит в построении выпуклой оболочки заданных точек, проверке, принадлежат ли все 5 точек выпуклой оболочке, и проверке для каждого i, существует ли точка пересечения прямых A_iAi + 1 и A_i + 2A_i + 3 и лежит ли она по разные стороны с точкой A_i (или любой другой из трёх оставшихся точек) от прямой A_i + 1A_i + 2 (сложение в индексах производится по модулю 5). Если какая-то из проверок не прошла — ответ No, иначе ответ Yes.

Задача E. Кодирование

Если найти соответствующие p и q невозможно, то f(x) — перестановочный многочлен по модулю 2^m (то есть он переводит последовательность из целых чисел от 0 до 2^m - 1 в какую-то их перестановку).

Рассмотрим некоторые свойства перестановочных многочленов.

• Если m = 1, то сумма всех коэффициентов, кроме свободного члена, обязана быть нечётной. Иначе f(0) = a₀ и f(1) = a₀ + (a₁ + a₂ + ... + a_n) имеют одинаковый остаток от деления на 2, и многочлен перестановочным не является.

• Если многочлен является перестановочным по модулю 2^m, то он является перестановочным и по модулю 2^m - 1. Пусть это не так, тогда существуют два таких числа p и q (0 ≤ p, q < 2^m - 1), которые дают одинаковые остатки f(p) и f(q) от деления на 2^m - 1. Рассмотрим числа p, q, p + 2^m - 1 и q + 2^m - 1. Значения f(p + 2^m - 1) и f(p) имеют одинаковые остатки от деления на 2^m - 1: вычтем полиномы друг из друга и заметим, что разность делится на 2^m - 1. Аналогично сделаем для f(q + 2^m - 1) и f(q), то есть получаем четыре числа f(p), f(q), f(p + 2^m - 1), f(q + 2^m - 1), которые дают различные остатки от деления на 2^m и одинаковые — на 2^m - 1. Но таких чисел может быть не более двух. Противоречие.

• Если многочлен является перестановочным по модулю 2^m и m > 1, то a₁ нечётно. В самом деле, пусть a₁ чётно. Тогда берём p = 0 и q = 2^m - 1. Легко видеть, что f(q) = a₀ + a₁·2^m - 1 + a₂·2^2m - 2 + ... + a_n·2^nm - n = f(0) + (a₁ / 2)·2^m + 2^m·r, где r — целое число (так как при m > 1 k(m - 1) - m ≥ 0), тем самым f(p) и f(q) дают одинаковые остатки от деления на 2^m, что противоречит свойствам перестановочных многочленов.

• Рассмотрев примеры для m = 2 и m = 3, можно заметить, что у перестановочных многочленов сумма коэффициентов при чётных степенях оказывается чётной. Это утверждение верно и для более высоких m; более того, перечисленные свойства являются необходимыми и достаточными. Полное доказательство можно найти в англоязычной статье Ronald R. Rivest.

Таким образом, всё, что вам нужно — это проверить, что сумма a₁ + a₂ + a₃ + ... + a_n нечётна, и что при m > 1 к тому же a₁ нечётно, а сумма коэффициентов при чётных степенях чётна. Если эти требования выполняются, то ответом будет No (то есть многочлен перестановочный, и требуемых p и q найти нельзя). Иначе ответ — Yes.

Задача F. Плейлист в будущем

Вначале найдём множество K вершин, принадлежащих к одной компоненте сильной связности, для которых верно следующее свойство: не существует ни одного ребра, которое начинается в вершине, принадлежащей этому множеству, и заканчивается в вершине, ему не принадлежащей.

Из ограничений задачи видно, что такое множество можно выбрать единственным способом, и оно будет содержать вершину 1. Найти это множество можно, например, поиском в глубину, начиная с вершины 1.

Очевидно, что после 10²⁰¹⁶ проигранных композиций вероятность исполнения композиции извне этого множества можно при требуемой в задаче точности считать нулевой (а 10²⁰¹⁶ — бесконечным количеством итераций).

Вектор вероятностей p после бесконечного количества композиций должен удовлетворять системе линейных уравнений pW = p, где W — матрица смежности подграфа, построенного на вершинах из множества K.

Таким образом, мы имеем однородную систему уравнений (W^T - I)p^T = 0 и нормирующее уравнение 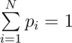. Довольно просто можно показать, что система всегда будет совместной; система может быть решена, например, методом Гаусса.

В качестве ответа в таком случае надо взять p₁.

P.S. Если вы заметили опечатку сообщите мне об этом личным сообщением.