Editorial for Round #118

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Ни одна из задач не была специально взята с "Wikipedia". Для меня было очень поразительно, что задача "B" была там.

A (Div 2). (Идея : Gerald, реализация : Aksenov239, код : 1670635)

Если длины строк не равны — то ответ "NO". Далее мы ищем позиции, на которых символы в строчках не совпадают. Если таких позиций не 2 — "NO". Иначе меняем 2 символа не этих позциях в первой строке, и сравниваем строки.

B (Div 2). (Идея : Aksenov239, реализация : Aksenov239, код : 1670637)

Можно заметить, что всё можно считать в целых числах, так как k — целое число процентов.
Для каждого гнома мы находим оптимальную стратегию — то есть проверяем 2 стратеги и выбираем лучшую.
А далее просто сортируем.

A (Div 1). (Идея : Aksenov239, реализация : Aksenov239, код : 1652592) Предположим, что после i-го года, у нас было x треугольников вверх и y треугольников вниз. После ещё одной итерации можно заметить, что количество треугольников стало — 3x + y вверх и x + 3y вниз. Рассмотрим разницу между ними: на i-ый год она равна x - y, а не i + 1-ый — (3x + y) - (x + 3y) = 2 * (x - y). Теперь ясно, что разница между количеством треугольников за год увеличивается в 2 раза. Так как на i-th год разница становится 2ⁱ и всего треугольников 4ⁱ. То на i-ый год количество треугольников, направленных вверх — 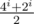$\text{[math]}$ . Это можно посчитать по модулю p, используя алгоритм быстрого возведения в степень.

B (Div 1). (Идея : Aksenov239, реализация : Aksenov239, код : 1652597) Ответ на эту задачу: 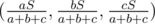$\text{[math]}$ .

Доказательство: 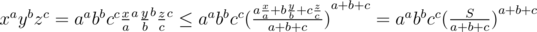$\text{[math]}$ . (Это неравенство о среднем арифметическом и среднем геометрическом. Для тех, кто желает ознакомиться.)

Равенство достигается только при 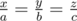$\text{[math]}$ .

Но надо не забывать про нули. Если a = b = c = 0 — вы должны выбрать какую-нибудь подходящую точку — x + y + z ≤ S.

C (Div 1). Без комментариев. :-)!

D (Div 1). (Идея : Aksenov239, реализация : cerealguy, Gerald, Aksenov239, код : 1652604)

Это задачка на теорию чисел.

Постараюсь объяснить всё по шагам:

1) Сначала докажем, что НОД чисел не больше 2.

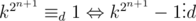Пусть $\text{[math]}$ . Возводим обе части в квадрат $\text{[math]}$ , а нам нужно, чтобы 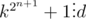$\text{[math]}$ . Это означает, что d может быть только 2.

2) Сделаем наше длинное произведение покороче.

$\text{[math]}$ .

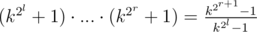Мы это можем посчитать по модулю p быстро, и поделить на 2^r - l, если k — нечётное.

3) Но есть несколько ловушек.

Первая — это не работает, когда p = 2 — но Вы справитесь сами.

Другая проблема посложнее, что если $\text{[math]}$ , это означает, что для любого i ≥ l : $\text{[math]}$ , из чего следует,
что для любого i ≥ l : k^2ⁱ + 1 ≡ _p2. И наше произведение по модулю p равно 2^{r - l + 1}.

E (Div. 1) (Идея : Aksenov239, реализация : cerealguy, код : 1652611)

Эту задачу не взяли на РОИ, поэтому я предложил её здесь. На мой взгляд, задача вполне сложная. Если честно, я точно не знаю, что написал cerealguy, но его решение работает за O(nlogn) — без бин-поиска. Для меня это достаточно уже сложно, так как первоначальное решение было с ним. (Вроде, даже такие решения прошли.) Также были ещё решения с более худшей асимптотикой, но некоторые даже быстрее работали.

Я могу Вам только дать ключевые идеи решения, которые Вам помогут. (В конце концов, вы можете посмотреть решение cerealguy)

Идеи:

Для каждого гнома найдём ближайшее метро. Это можно сделать за nlogn с помощью дерева отрезков или чего Вам там больше нравится.
Можно заметить, что если гном идёт до метро, то другие гномы с меньшим расстоянием до метро, могут тоже идти туда — это никак не повлияет на ответ. Поэтому отсортируем гномов по этому расстоянию.
Точки, до куда гном может дойти за t секунд, представляет собой ромб. И мы можем пересечь все ромбы за O(n) — пересечение будет похоже на прямоугольник.
Построим начальное пересечение, когда никто не идёт в метро. Мы получим прямоугольник.
Основная идея — для прямоугольника пересечения — ближайшее к нему метро всегда остаётся одним и тем же. Теперь можно пройтись по гномам в отсортированном порядке, мы умеем быстро пересчитывать прямоугольник пересечения — и поэтому можем быстро пересчитывать ответ.

И у нас получается решение за O(nlogn). Та-дамс!

Спасибо за Ваше внимание и понимание. Мне очень стыдно, за то что я натворил с задачей "C".

Комментарии (10)

Показать архивные | Написать комментарий?

Aksenov239

13 лет назад, # |

← Rev. 3 →

Временно ссылки с кодом недоступны.

Временная замена:

А div. 2 — http://pastie.org/3884140

B div. 2 — http://pastie.org/3884143

A div. 1 — http://pastie.org/3884145

B div. 1 — http://pastie.org/3884147

D div. 1 — http://pastie.org/3884149

E div. 1 — http://pastie.org/3884152

→ Ответить

For some time links for solutions isn't working. Temporarily:

ksdeol

great tutoriAL!!!!!!!!!!

stryan123

I just think cf need to save the draft as I accidently click on some link and the content is lost……

I may need to borrow a book about number theory……

and at last……I just can't understand the product in C(Div.1)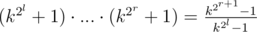

a rookie

chhung6

13 лет назад, # ^ |

Try this:

Multiply LHS by "k^(2^l) — 1" and get: (k^(2^l) — 1) (k^(2^l) + 1) ... (k^(2^r) +1)
Repeatedly apply the identity: (a — b)(a + b) = a^2 — b^2 (for every first two terms)

Sammarize

с более худшей асимптотикой =/

Mohamed_Ayman

9 лет назад, # |

A (Div 1) : simple explain

suppose : up -> num of upward triangle and down -> num of downward triangle
Initially : up = 1 and down = 0 then up = 3 and down = 1 then up = 10 and down = 6 then up = 36 and down = 28 then up = 136 and down = 120 then and so on ...
conculsion : each n we split each triangle to 4 triangles it's mean at n we have 4^n triangle we want to want how many of 4^n are upward
suppose : a -> num of upward triangle b -> num of downward triangle it's mean a + b = 4^n ----------------------> (1)
fact : at n=0 , up = 1 and down = 0 then at n=1 , up = 3 and down = 1 ratio is 3/1 then at n=2 , up = 10 and down = 6 ratio is 5/3 then at n=3 , up = 36 and down = 28 ratio is 9/7 then at n=4 , up = 136 and down = 120 ratio is 17/15 then and so on ...
conculsion : we see that ration of upward / downward => (2^n)+1 / (2^n)-1 so : a' = [ (2^n)+1 ] , b' = [ (2^n)-1 ] -------> (2) so : a'c + b'c = 4^n ----------------------> (3) such that c is constant we want to know a'c ?
also we see that sum of a' + b' = [ (2^n)+1 ] + [ (2^n)-1 ] a' + b' = [ (2^n)+1 + (2^n)-1 ] a' + b' = [ 2*(2^n) ] a' + b' = [ 2^(n+1) ] ------------------> (4)
from (2) : a' = [ (2^n)+1 ] , b' = [ (2^n)-1 ] from (3) : a'c + b'c = 4^n we want to know a'c ?
[ a' + b' ] * c = 4^n from (4) : a' + b' = [ 2^(n+1) ]
[ 2^(n+1) ] * c = 4^n so c = 4^n / 2^(n+1) c = 2^(2n) / 2^(n+1) a'c = [ (2^n)+1 ] * 2^(2n) / 2^(n+1) a'c = [ 2^(3n) + 2^(2n) ] / 2^(n+1) a'c = 2^(2n-1) + 2^(n-1)

← Rev. 5 →

suppose : up -> num of upward triangle and down -> num of downward triangle
Initially :
up = 1 and down = 0 then
up = 3 and down = 1 then
up = 10 and down = 6 then
up = 36 and down = 28 then
up = 136 and down = 120
and so on ...
conculsion : each n we split each triangle to 4 triangles it's mean at n we have 4^n triangle we want to want how many of 4^n are upward
suppose : a -> num of upward triangle b -> num of downward triangle
it's mean a + b = 4^n ----------------------> (1)
fact :
at n=0 , up = 1 and down = 0 then
at n=1 , up = 3 and down = 1 ratio is 3/1 then
at n=2 , up = 10 and down = 6 ratio is 5/3 then
at n=3 , up = 36 and down = 28 ratio is 9/7 then
at n=4 , up = 136 and down = 120 ratio is 17/15
and so on ...
conculsion :
we see that ration of upward / downward => (2^n)+1 / (2^n)-1
so : a' = [ (2^n)+1 ] , b' = [ (2^n)-1 ] -------> (2)
so : a'c + b'c = 4^n ----------------------> (3)
such that c is constant
we want to know a'c ?
also we see that sum of a' + b' = [ (2^n)+1 ] + [ (2^n)-1 ] ,
a' + b' = [ (2^n)+1 + (2^n)-1 ] ,
a' + b' = [ 2*(2^n) ] ,
a' + b' = [ 2^(n+1) ] ------------------> (4)
from (2) : a' = [ (2^n)+1 ] , b' = [ (2^n)-1 ]
from (3) : a'c + b'c = 4^n
we want to know a'c ?
[ a' + b' ] * c = 4^n
from (4) : a' + b' = [ 2^(n+1) ]
[ 2^(n+1) ] * c = 4^n
so c = 4^n / 2^(n+1)
c = 2^(2n) / 2^(n+1)
a'c = [ (2^n)+1 ] * 2^(2n) / 2^(n+1)
a'c = [ 2^(3n) + 2^(2n) ] / 2^(n+1)
a'c = 2^(2n-1) + 2^(n-1)

Kar98k

6 лет назад, # |

I solved Div1 B using Lagrange's Multiplier .

L(x,y,z,lamda)=x^a*y^b*z^c-lamda*(x+y+z-s) and then partially differentiating w.r.t x,y,z and equating to 0 gives x=a*s/(a+b+c) y=b*s/(a+b+c) z=c*s/(a+b+c)

sid779

5 лет назад, # |

AM — GM Inequality updated link for DIV 1-B

Блог пользователя Aksenov239