Для каждого друга смотрим, будет ли его высота больше h. Если да, то его ширина — 2, иначе — 1.
Complexity O(n).
677B - Ваня и кухонный комбайн
Решение, которое просто делает то, что описано в условии, не пройдет, т.к. если высота каждой картофелины будет 109, а скорость измельчения — 1, то на каждую картофелину будем тратить 109 операций.
С каждой новой картофелиной высотой ai будем измельчать картофель до высоты ai MOD k, тогда мы будем тратить на это a[i] / k секунд. Если мы не можем засунуть после этого новую картофелину, то мы потратим еще 1 секунду, иначе просто положим эту картофелину. Мы получим такой же ответ, как бы если мы делали то, что описано в условии.
Асимптотика O(n).
Переведем слово в 2-ичную систему счисления, это сделать легко, так как 64 — степень двойки. Проходимся по битах этого числа: если бит равен 0, то у нас может быть 3 различных варианта этого бита в нашей паре слов: 0&1, 1&0, 0&0, иначе только один вариант: 1&1. В таком случае результатом будет 3nullbits, где nullbits — количество нулевых битов.
Асимптотика O(|s|).
Сделаем динамику dp[col][row], где dp[col][row] — минимальное время, которое нужно для того, чтобы открыть сундук в клетке (col, row). Для клеток цвета 1 dp[x][y] = x + y. Для каждого следующего цвета color будем перебирать все клетки цвета color - 1 и все клетки цвета color, тогда для каждой клетки цвета color с координатами (x1, y1) и клетки цвета color - 1 с координатами (x2, y2) dp[x1][y1] = dp[x2][y2] + abs(x1 - x2) + abs(y1 - y2).
Но этого решения будет недостаточно, так как его асимптотика — O(n2·m2)
Можем сделать такое улучшение: пусть cnt[x] — количество клеток цвета x, тогда когда cnt[color]·cnt[color - 1] ≥ n·m, можно сделать поиск в ширину от клеток цвета color - 1 к клеткам цвета color.
В таком случае будет асимптотика O(n·m·sqrt(n·m)).
Также есть решение с использованием двухмерного дерева отрезков:
Для каждой клетки (x, y) в таблице возьмем максимально возможный крест, в котором не присутствуют нули. Чтобы сделать это быстро, сохраним массивы частичных сумм для всех возможных 8 направлений, где каждая клетка будет обозначать количество ненулевых шариков в каждом из направлений. Например для того, чтобы узнать, сколько ненулевых шариков находится справа от клетки (x, y), создадим массив p[x][y], в котором p[x][y] = p[x][y - 1] + 1 если a[x][y]! = 0 иначе p[x][y] = 0
Таким образом для каждой клетки (x, y) мы можем найти крест максимального размера, в котором не будет нулей.
Мы можем сравнить значения произведений для крестов в координатах (x, y) и с радиусом r, воспользовавшись логарифмированием. К примеру, если нам нужно сравнить кресты с значениями x1·x2·...·xn и y1·y2·...·ym, мы можем сравнить log(x1·x2·...·xn) и log(y1·y2·...·yn), что будет эквивалентно сравнению log(x1) + log(x2) + ... + log(xn) и log(y1) + log(y2) + ... + log(ym).
Таким образом для нахождения значения log(x1) + log(x2) + ... + log(xn) для каждого креста мы можем аналогично хранить массивы частичных сумм для каждого с направлений и для каждой клетки (x, y) искать максимальное значение креста с центром в ней за O(1).
Итоговая асимптотика O(n2).
Human drinks a Vampire's blood. Out of curiosity, the Vampire asks what it tastes like.
"It's irony."
How is this possible to prove time complexity in 677D - Vanya and Treasure ?
I finished the problem C ten seconds after the contest... :'(
I enjoyed this round... Thanks.
There's a bit of Russian in the English version of the description for C:
"В таком случае результатом будет 3nullbits, где nullbits — количество нулевых битов."
Someone Please Post the code for all the problems.Please!!!!
You can see everyone's code in the standings page
Tysm
That editorial has been blazingly fast!
And so is the ratings update
Thanks for fast editorial.
I liked 677D - Vanya and Treasure the most and I want to share my approach, also in O(n3).
Let's iterate over value v from 1 to p - 1. Let's say that for each cell with this value we know how fast can we get here and open this cell. Now, we want to calculate the same for cells with value v + 1.
For each row y if there is at least one cell in this row with value v, then let's iterate over cells in this row: once from left to right, once from right to left. We want to consider moving from one of cells with value v in this row, to any cell with value v + 1, not necessarily in this row. So, let's keep a variable best as we iterate over cells in the row — how quickly can we get to the current cell (with assumption that we already were in a cell with v in this row).
To update best we must: 1) increase it by 1 when we move to the next cell in the row, and 2) if the current cell has type v then do
best = min(best, dp[cell])(wheredp[cell]means how fast we can get here from the start).And we must use best to find dp values for cells of type v + 1. As we iterate of cells in the row y, for each x we must iterate over all cells of type v + 1 in column x and for each of them update dp using best, i.e.
dp[cell] = min(dp[cell], best + abs(y - cell.y)). By doing it we consider moving from any cell of type p somewhere on the left to any cell in column x. Remember that you need to iterate second time from right to left (first iteration was from left to right).code: 18192113the same code with some comments added, should be easier to read: 18203850
Thanks for posting your solution, I'm trying to understand it.
Thanks in advance.
For me the x axis goes from left to right. Sorry if it confused you. So, x denotes column for me.
You must think about the amortized complexity. For each cell in vector of cells
odw[v](v denotes type) how many times it can appear (how many times it can be processed). Turns out that we process it once for each row y when we consider going from type v to type v + 1. There are n rows and thus we process each cell there at most O(n) times. So, the amortized complexity is O(n3).Thanks for sharing, amazing solution. But I still don't understand why the complexity is O(n^3). when going from type v to type v+1, it does visit O(n) times cells of type v+1 and visit only once cells of type v, but for each row y, each cell of this row of other types is visited too.
I understand it. Since each row has O(m) different types, each row will be scanned O(m) times, so there is O(mnm) best update operations and O(nmn) dp update operations.
Does the use of the 'visited' array change the complexity? If not, how/why did you come with such heuristic, if I may call?
By the way, pretty neat. How do you come with such solutions?
Yes, it does. Consider any particular cell arr[i][j] in the matrix. How many times will it be processed? O(n) times, where n = number of rows. And there are n*m total cells. So complexity comes out to be O(n*n*m). But I am not sure about this. Please let me know if this is incorrect.
Think about a test where all cells have different types. Then, without
vis[]we have O(n4) because for each of n2 types we will iterate over x and then over y. But, with usingvis[]we can get to the last loop only once for each cell, so it's amortized O(n3).I see... I have an intuitive feeling that this is right, but I can't think properly about the amortized complexity. I will spend some more time thinking on this. Thanks for the help!
To update
dp[cell]of v+1, I think the formule should bedp[cell] = min(dp[cell], best + abs(y - cell.y))since
xandcell.xare equal.You are right, thank you very much. I've just corrected my comment, it's ok now.
А как строго доказывать асимптотику в D? Для случаев, когда cnt[color-1], cnt[color] < n*m. Почему они суммарно не превысят n*m*sqrt(n*m)?
Да, задача очень крутая, давно таких не было.
Можно сказать, что bfs делается, когда хотя бы cnt[color] или cnt[color — 1] больше корня.
Тогда док-во будет очевиднее (при переборах каждую мы переборем не более 2sqrt(nm) раз
Для ровно такого решения тоже можно доказать: будем говорить, что мы перебираем пары такие, что первый элемент того цвета, которого меньше. Тогда каждый элемент будучи вторым встречается не более корня раз суммарно
Ошибся
My solution for D is O(nmlog2(nm)). The basic idea is the following: define dp[r][c] analogously to the above definition.
Let's fix some chest at (r, c), and suppose that the previous chest we visited is at some position (r', c') with r' ≤ r and c' ≤ c, then dp[r][c] = dp[r'][c'] + (r - r') + (c - c'). Notice that we can split this into r + c and dp[r'][c'] - r' - c'. Similarly, suppose that we had r' ≥ r instead, then dp[r][c] = dp[r'][c'] + (r' - r) + (c - c') which splits into c - r and dp[r'][c'] + r' - c'.
This gives us the following recurrence:
dp[r][c] = min(topleft, topright, bottomleft, bottomright)
Where:
topleft = r + c + minr' ≤ r, c' ≤ cdp[r'][c'] - r' - c'
topright = - r + c + minr' ≥ r, c' ≤ cdp[r'][c'] + r' - c'
topleft = r - c + minr' ≤ r, c' ≥ cdp[r'][c'] - r' + c'
topleft = - r - c + minr' ≥ r, c' ≥ cdp[r'][c'] + r' + c'
.. with the additional constraint that the chest at (r', c') is has a key one less than the key at (r, c). What you'll notice is that each of these four values can be phrased as a range minimum query in some square (depending on r and c) plus/minus r and c. We can thus store all values after the 'min' in four distinct 2D Fenwick trees (one for all four directions).
So in the first 2D Fenwick tree we'll store dp[r'][c'] - r' - c' at (r', c'), etc. Then we can simply query the answer for each (r, c).
Notice that each time you 'finish' a type of key, you would want to reset the Fenwick trees such that they don't contain the values of smaller types of keys. If we'd reset naïvely, each reset would take O(nm) time, but you can speed this up by only resetting the positions that contain a value (this probably sounds a bit odd, see my code for reference, i.e. the
reset_aroundmethod).Code: 18198603, ~200ms.
Considering p <= nm you may remove it from complexity
Right, thanks :)
I did the same, but I fixed r' so I did not need to worry about abs(r' - r). Then you can simply keep 2 fenwick trees per row of the grid ordered by the c' values.
The complexity --> O(N * M * N * logM)
Code -> 18197729 (It passes in 1.3 seconds)
Or you can do the same with binary search.
18202438
Yes, this is much better. I should think twice before smashing data structures into my code :P
I think your approach can be also simplified a little (not everyone is familiar with 2D segment trees), and you get rid of one log factor:
The step from 1D to 2D Fenwick trees is nothing more than duplicating a for loop and renaming some variables, you don't really need to understand it, just realize you can do 2D range queries :)
Having said that, I do like your simplification, thanks for sharing!
EDIT: Also, just to be clear, there's no lazy reset or something like that going on, I just follow the query path for (r, c) and reset all values on the path, for a total amortized cost of O(nmlognm) for the entire solution.
".. with the additional constraint that the chest at (r', c') is has a key one less than the key at (r, c)"
How do you ensure this in your query?
See the last paragraph.
Some notes about D: submissions of only 33 official participants had passed sys.tests
I wrote an overly complicated solution for problem D involving four 2D BIT's, one for each quadrant, each with its separate update and query functions.
Then I processed the cells in ascending order of key, updating the four BIT's and resetting them as necessary.
I think total complexity is O(N * M * log2(max(N, M))), which is slightly better than the model solution from this editorial.
Here's my submission for further clarity: 18195269
One can solve D in O(N*M*log^2(N*M)). The idea is like the DP one from the editorial.
We start by iterating all points starting from the one with the smallest number. We also build four 2d minimum segment trees on the points from the previous type.
We have four cases (let our point be x, y):
dp[x][y] = dp[x'][y'] + x - x' + y - y' = (dp[x'][y'] - x' - y') + (x + y)Now in the first 2d segment tree we have to update all points from the previous type (x', y') value to (dp[x'][y'] — x' — y'). So now for a point of the current type the answer is minimum in rectangle [1, 1] to [x; y] + x + y. This is a simple 2d segment tree with range query and point update.
We do four cases of this type:
X < x'; Y < y'
X > x'; Y < y'
X < x'; Y > y'
X > x'; Y > y'
We do N*M point updates and N*M range queris so the complexity is O(N*M*log^2(N*M)). In fact this can be done with not a 2d segment tree but with a 2d minimum BIT, because all of our queries are of a prefix/suffix rectangle.
That's exactly what I did! I thought I was the only weirdo doing that xD!
I believe the complexity is actually O(N * M * log2(max(N, M))).
O(log(nm)) and O(log(max(n, m)) is one thing, actually
As well as O(log(n + m))
What do you mean?
For example, if N = M = 1000, then log(N * M) = 20, while log(max(N, M)) = 10. In general, if N = M, then log(N * M) = 2 * log(max(N, M)).
Are you familiar with O-notation?
log(max(n, m)) <= log(mn) = O(log(mn))
log(mn) <= log(max(m,n)^2) = 2 log(max(m, n)) = O(log(max(m, n))
If f(n) = O(g(n)) and g(n) = O(f(n)) then h(n) = O(f(n)) <=> h(n) = O(g(n))
Well I also did think it's weird and I was 100% sure I overkilled it :D
About the complexity, I think it should actually be O(N*M*logN*logM).
Could Someone plz explain Div2 C in detail. if our word is "0125" then how will we write it's binary representation and why is the answer 3^(total zero bits)
Firstly, you should understand, that for each character in string there is a number. So "0125" is actually the same 0 1 2 5, now we should translate it to 2 base system. So it will be 000000 000001 000010 000101 . You should remember to add zeros till length is 6, cause max number in 2cc has 6 numbers. Now we should mention that 1 appears from pair 1&1 , however 0 there are 3 pairs: 0&0, 0&1 , 1&0. So now we just need to count how many zeros are there and print 3^cnt. P.S.Sorry for my English
I think my solution for C is more natural.
I precalculated values A[i], which means how many pairs of characters are there such that their AND is equal to i. We can do this by just trying all 64 * 64 possible pairs. Then we just multiplicate all these values for every character of S and we're done.
Here's my submission: 18190366
sorry to ask a foolish question but could you plz explain the meaning of the the question with example.Although i understood your solution but still i wanted to understand the question clearly. Thanks
How about solving D by shortest path algorithms, such as Dijkstra? Just model the palace as a graph, and cells with color C will be connected to cells with C+1. We set a dummy starting point (0,0) and it can be connected to itself if (0,0) has color 1. I haven't started to practice on graph problems so I don't know how to implement this algorithm. But I understand the theory and I think Dijkstra can solve it. The complexity is VlogV+E, where V = n*m. E is also n*m since each cell only have at most one edge out. So total complexity is (n*m)log(n*m). Please correct me if you find this is impossible.
If you want to connect cells of color C with cells of color C+1, then you will get (n·m)2 edges.
Ah, thanks for this! I was wondering why my code got MLE.
It's solvable with Dijkstra 18210389
I connected 1 with 2(all the positions). 2 with 3 and so on. Then I worked with bfs but I got TLE in 19th tcase. though I'm bit confused about my solution complexity, would you please tell me why my solution got TLE?
code: http://ideone.com/1Tum2W
My solution which I failed only because the limits in To was improperly set.
I am checking only 2 Chests for every row and every column for updation of dp array of chest with key x, the reason being every other Chest with number x+1 will be useless as at least one of these points give the same result .
I don't know why won't CF give me Purple.
18203988
Link to Image
More Explanation: As In normal dp for a chest with number x ,
we had to relax for every chest with number x , every chest number with x+1.
Now my observation for bringing complexity down was that for dp[u] = min{dp[v] + dist(u,v)} where v has a chest number x+1 was that the system was a grid.
Now we can imagine a rectangle around the point. Amongst every rectangle we will take the smallest.
Now for relaxing , we need to check only these points! which are simply (N+M). So for every point we check only (N+M) points.
Which causes the complexity to be N*M*(N+M).
Note the figure surrounding won't be a rectangle always . Like this http://postimg.org/image/4c7e5k5nv/ Note: The black dot is a point with chest number x , I am brute forcing on the points that surround it.(Not necessarily they all will exist).
Note : You will need to see the tricks I used to optimize memory too.
Why did the rectangle thing works : as every point outside this rectangle will have to pass through this border , hence the shortest path existing will be surely one of these points for sure.
dude nice approach. love it:)
You surely get the minimum distance from the points of chest x-1 to the points of chest x.
Where are you taking care of the distance already covered uptill points of chest x-1 , which also gets added to compute dp[i][j].
I am only considering the points surrounding my point to minimize whole function that is
distance[i][j] = minimum of(distance[x][y] + distance of Point({x,y},Point u)
Here {x,y} are the points surrounding the point {i,j} in a convex hull/rectangle ( I ain't getting the correct word to use, that's why I built a pic).
Could you please explain why it won't happen that you will incorrectly find maximum of logarithms due to rounding errors in last problem?
We wonder if a·log(2) can be close to b·log(3). We know that a and b are positive integers up to 1000.
On the left we have a rational number with denominator up to $1000$. On the right (omitting epsilon) we have a non-rational number which is kind of simple — it doesn't look like especially designed to be close to some rational number with small denominator. We must use this kind of strange explanation because some other non-rational number could be much much closer. So, for this "kind of simple" non-rational number, I would say we should expect it won't be closer than ε = (1 / 1000)2 to some rational number with denominator ≤ 1000.
Thanks, yep, it seems that for this particular problem we may just iterate through a, b and see that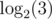
is not close enough
Let's use the magical power of computers!!!1!1
http://ideone.com/bzgKY1
So 21054 and 3665 are pretty close.
it's only 4e-5, not so close.
Yes, the 'close' was mostly sarcastic :P
In fact, the difference is 'only' a 313-digit number! http://www.wolframalpha.com/input/?i=2^1054+-+3^665
Wild_Hamster Please explain in problem E how the complexity of the code is O(n^2) . It is understood that the traversing of the grid is O(n^2) but when we precompute using the for loop, how is that being incorporated in O(n^2).
For D, can anyone explain the following? "We can do such improvement: let cnt[x] be the amount of cells of color x, then when cnt[color]·cnt[color - 1] ≥ n·m, we can do bfs from cells of color color - 1 to cells of color color. Then we will have complexity O(n·m·sqrt(n·m))." I really have no idea how sqrt come out
Suppose a modification of this algo:
You iterate through pairs if both cnt's are <= sqrt(nm) and do bfs otherwise.
Now bfs is run no more than 2 * sqrt(nm) times and each element consist no more than in 2 * sqrt(nm) pairs you iterated.
It may also be proven for original solution too but it's a bit harder to explain (you may try it yourself)
but how to prove the dynamic programming part's complexity is <=O(nm*sqrt(nm))?
please view my reply to kouytoupa below
thank u
a + b >= 2*sqrt(a*b), so 2*m*n = 2*sum(cnt[x]) > (cnt[1] + cnt[2]) + (cnt[2] + cnt[3]) + .. + (cnt[p — 1] + cnt[p]) >= 2*sqrt(cnt[1]*cnt[2]) + 2*sqrt(cnt[2]*cnt[3]) + ...
If there are more than sqrt(m*n) "x x+1" pairs such that cnt[x]*cnt[x + 1] > m*n: 2*m*n > sqrt(m*n) * 2*sqrt(m*n) + ... This can't be true. So bfs will be called no more than sqrt(m*n) times.
but how to prove the dynamic programming part's total complexity is not greater than nm*sqrt(nm)?
i just know every cnt[x]*cnt[x+1]<=nm in dp part's, but in total, there may be more than sqrt(nm) of pairs, thus i can't prove the total complexity is <=nm*sqrt(nm)
and of course, when pairs number is >sqrt(nm), surely there exists some pairs of 'x x+1', such that cnt[x]*cnt[x+1]<nm, the product cannot reach nm, but still, how to prove that the total complexity of dp part is <=O(nm*sqrt(nm))?
O(c(cnt1*cnt2)+c(cnt2*cnt3)+...) <= O(p*c(nm/p)^2) where c(x)=x<nm?x:nm. The maximal value is when p=sqrt(nm), so O(p*c(nm/p)^2)<=O((nm)^1.5).
why is c(cnt1*cnt2)+... < p*(c(nm/p)^2)?
according to am-gm inequality, i just know that, (c(cnt1*cnt2)+...)/(p-1)<=(c(cnt*cnt2)*...)^(1/p)<=mn ,therefore c(cnt1*cnt2)+...<=(p-1)mn<pmn
i cant get that c(cnt1*cnt2)+...<=p*c(nm/p)^2
oh i made a mistake
am-gm inequality suggests that (c(cnt1*cnt2)+...)/(p-1)>=(c(cnt*cnt2)*...)^(1/p)
For the dynamic programming part:
cnt[x]*cnt[x + 1] = min(cnt[x], cnt[x + 1]) * max(cnt[x], cnt[x + 1]) <= m*n so min(cnt[x], cnt[x + 1]) <= sqrt(m*n).
Then sum(cnt[x]*cnt[x + 1]) <= sqrt(m*n)*(max(cnt[xt1], cnt[xt1 + 1]) + max(cnt[xt2], cnt[xt2+1]) + ...) <= sqrt(m*n)*2*sum(cnt[x]) <= sqrt(m*n)*2*m*n.
why is cnt[x]*cnt[x+1] <=mn?
the code just implies that when cnt[x]*cnt[x+1]>mn, then it will go to bfs instead, but cnt[x]*cnt[x+1] can be >mn
So it will go to dp only if cnt[x]*cnt[x + 1] <= mn.
Actually, cnt[xt1]*cnt[xt1+1], cnt[xt2]*cnt[xt2+1],... (cnt[xti]*cnt[xti + 1] <= mn here) is a subsequence of cnt[1]*cnt[2], cnt[2]*cnt[3], ...
thank u
Опубликуйте, пожалуйста, авторское решение задачи 677D - Ваня и сокровище на языке Java. Я, как ни старался, не смог преодолеть TL 47, интересно посмотреть как можно ускорить решение.
Немного похачил ваше решение – самые весомые ченджи — PQ -> DEQ + Item -> Point 18205996
PS: А если пофиксить мою багу с добавлением в очередь, то становится еще получше 18206697
Мне в итоге помогло PQ -> DEQ + Item -> Item[] + Item и ещё немного покрутить константу (n * m * 5).
Очень интересно, всё-таки, посмотреть на авторское решение, которое укладывается в 1.5 секунды с двухкратным запасом.
can anyone please prove the complexity of the first solution of problem D ? why such improvement can optimize the complexity to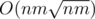
Can someone provide a counter-test?
http://codeforces.net/contest/677/submission/18202030
This solution considers only top rows with cells of type 2 but in the optimal solution we should use a cell of type 2 in the last row. The optimal answer is 15, this solution prints 17.
Unfortunately, it's almost impossible for a setter to predict this kind of crazy heuristic. So he shouldn't be blamed for that.
Thanks. :) (Y)
in Problem C, when i tranform V_V into decimal it is 31 + 63*64 + 32*64*64 then into binary 11111111111011111 yet it contains 1 ZERO only, so the answer should be 3, and the answer for it is 9, can someone explain how come?
You need to look it bit-by-bit.
V is 31 -> 011111, it can have 3 possible pairs of bits, right? 011111 AND 111111, 111111 AND 011111, 011111 AND 011111.
_ is 63 -> 111111, so only one possible pair of bits -> 111111 AND 111111
So, we have 3 * 1 * 3 = 9
Code
Hey,
What is the meaning of this sentence : ' he used & as a bitwise AND for these two words represented as a integers in base 64' . Is base in this sentence same as radix.
Thanks in advance.
Radix = the base of a system of numeration.
So don't you think that two words represented as integers in base 64 is a bit ambiguous??. I think it should be more like.
Each character is represented as an integer in base 64.
What do you say?
Thanks in advance
Sometimes problem is not only about solving :) You have to understand it too
Actually, you must form a block of 6 bits for every base-64 character, and this includes leading zeroes.
31 is 011111 and 63 is 111111, so the final number will be 0111111111110111111, and there are two zeros.
we convert the base 64 string to binary by just converting the individual characters to binary and concatenating. but why this method doesnt work for base 10.
for base 64 string V_V, the decimal value of characters are 31, 63 and 31. so we can convert it to binary by writing
011111(31),111111(63) and011111(31), ie0111111111110111111.but if we try same method for base 10, number 42,
4 = 0100 in binary and 2 = 0010 in binary, but 42 != 01000010 in binary.
sorry if its a stupid question but i cant understand it.
That's because 64 is a power of 2 and 10 is not.
thanks.
Actually you can think less and forget about converting string to binary :)
Code
Could someone please explain the reduction used in problem D ?
and how to BFS when the starting points in color-1 each has its own distance from (1,1)?
it looks like it becomes weighted and i don't see BFS working anymore
what am i missing ?
It's not weighted because the edges still have length 1. You can apply BFS with a small modification: instead of adding 'color-1' points to the initial wave, you add them into the waves corresponding to their distance from (1,1).
I still don't understand it. We are in lvl x, and we want to do bfs from lvl x-1.
These fields have different distance from (1,1). The main idea of bfs is that it inserts filed to the queue as soon as it reaches it.
So for example distance between (1,1) and (x1,y1) = 43 and dist between (1,1) and (x2,y2) = 50.
You inserted both fields to the queue — first (x1,y1) second (x2,y2). Then you run bfs and it turned out that (x2,y2) reached field (x3,y3) faster (let's say in 2 moves) than (x1,y1) — it would reach it in 4 moves. So when you reach (x3,y3) you would set 50+2 = 52 distance from (1,1) instead of 43+4 = 47.
Edit: Maybe the solution will be to hold (x2,y2) until we stop processing fields with distance < 50 and then add it to the queue.
What am I missing?
In the normal BFS: we add some vertices in wave 0 (distances to them are 0). Calculate their neighbors — they become wave 1 (distances to them are 1). Continue like this: neighbors of vertices in wave k become wave k + 1 (unless they have already been visited).
In the modification: the first 42 waves are empty. Wave 43 is empty too, but we add (x1,y1) to it. Continue as in normal BFS, but add (x2,y2) to wave 50 (unless it has been visited already), and so on.
Thanks — I was about to edit my post. It's good to ask the question as quite often the answer just comes to your mind :)
I would simply hold (x2,y2) until I finish processing all the vertices with distance < 50 and then add it to the queue.
Can anyone tell how BFS is used to solve D?
I join the question. Can anyone explain it? Thanks.
Problem D is similar to this problem from ACM ICPC Polish regionals: http://main.edu.pl/en/archive/amppz/2012/biu
You can formulate the same dynamic programming and solutions to D with complexity around O(nm log nm) would pass. What is interesting is that in the problem I've given you want to maximize the distance you travel, not minimize it, and if you observe something more, you can go down to a very simple O(nm) solution.
I'm allergic to floating point numbers, so in E I did the following:
All we need to do is to compare numbers of the form: (2^a)*(3^b). In other words, we have to determine whether (2^a)*(3^b) — (2^c)*(3^d) is positive or not.
if a>=c and b>=d it is obviously true
if a>=c but b<=d then we can transform it to:
(2^c)*(2^(a-c)*(3^b) — (3^d)) = (2^c)*(3^b)*(2^(a-c)-(3^(d-b)).
It is positive only if (2^(a-c)-(3^(d-b)) is positive. So it is sufficient to determine whether 3^y >= 2^x for x,y<=1000. To do this, I need a function f(x) = smallest y so that 3^y >= 2^x. You can easily precalculate it, I just wrote a simple Python program, taking advantage of its big number arithmetics.
Or to write, without cheating, big integers in any language. You can calculate 3^0, 3^1, ... as binary numbers. For each 3^y the position of last bit is the largest power of 2 not increasing it.
Hi It would be great if in the second question it was explicitly mentioned that the order of pieces of potatoes must be maintained strictly. I couldn't do the question because for me it wasnt clear that the order should be maintained. The word 'next' used in the text is ambiguous. It also means another potato.
The following words were sufficient I guess: "He puts them in the food processor one by one starting from the piece number 1 and finishing with piece number n."
For 5 potatoes, the said statement doesn't imply that 1->3->2->4->5 is not a valid traversing. It is one by one and starts with 1 and ends with n.
I did think of the editorial solution but I did not submit it, thinking that it is too easy, along with the fact that aforementioned ambiguity exists. I figured out an alternate solution.
It would be to choose any permutation of 1 to n, starting with 1 and ending with n. Calculate the answer for it using the method in the editorial. It doesn't yield a unique solution, but it doesn't have to.
Sorry for being alarmingly pedantic, but given that it is my first contest I thought the question has to be tough and during the contest I thought it would require some dynamic programming concepts that I probably don't understand. I could have had a bit better initial rating had I submitted this solution.
please come up with alternative solution (other than tutorial) to problem B ?
You can precalculate an array m:
g(i, 0, 63) g(j, 0, 63) ++m[i & j]; Now you get there arem[i]pairs which couldandintoi. So you go through the string and mul up every element.could not get,if you could explain it a bit precisely.
The key is that you calculate how many(m[x]) pairs could form x before you go through the string. Code: http://codeforces.net/contest/677/submission/18207855 Hope it helps.
I'll share my approach which I hope is quite easy to follow. I simply used the relation:
height_of_potatoes_left_in_mixer + height_of_next_potato — k*t <= h
using this relation you can find the minimum time taken to smash just enough height of potatoes in the mixer so that the next potato can be added. There's a small catch however, while subtracting the height in mixer may go negative. To take care of this just make the height 0 when it turns negative before you add the next potato. Summing this time up for all n potatoes you will get the final answer. My code Hope it helps :)
Please help could not understand the editorial for problem D. Why is dp[x][y] = x+y for cells of color 1 ? Also explain the optimization approach !
dp[x][y]=x+y when a[x][y]=1 because the starting point is (1,1) as explicitly mentioned in the problem statement. As for the optimization, performing DP is O(|S1||S2|+|S2||S3|+...+|S(p-1)||Sp|) where Sk is the set of a[i][j]==k. However, this can lead to O(n^2 m^2) complexity in the worst case. Methods like Fenwick tree, etc. can lower the complexity to O(nm^2 lg(n+m)) or O(nm lg^2(n+m)) or O(nm lg(n+m)) depending on the implementation. The solution given by the problem authors is for each of the |Sk||S(k+1)| operations, performing BFS instead or comparing each pair has a maximal complexity of O(nm), providing an upperbound to each of the (p-1) calculations. As a result, this lowers the complexity from O(p*(nm/p)^2) to O(p*c(nm/p)^2) where c(x)=x<nm?x:nm. Then the worst case condition of p=2 no longer becomes maximal, instead becoming sqrt(nm) which lowers the total complexity to O((nm)^1.5).
So I have tried the DP/BFS solution and a Segment Tree solution for problem D. I have time limit with both solutions. It there any way to have AC in Java for this problem?...
http://codeforces.net/contest/677/status/D filter by language
ж
can anyone help me with 677 D vasya and fence im ade the O(n^2*m^2) algorithm but i am not getting this line:
We can do such improvement: let cnt[x] be the amount of cells of color x, then when cnt[color]·cnt[color - 1] ≥ n·m, we can do bfs from cells of color color - 1 to cells of color color. Then we will have complexity O(n·m·sqrt(n·m)).
PLs can someone explain
Нет ли в первом решении задачи про сокровища в пускании волны ошибки? Точки с прошлой итерации добавл-ся при испускании волны из точки с дистанцией val: while (pointer < lst.size() && lst[pointer].X <= val) bfs.push_back(lst[pointer++]);
Если из текущей точки приходим в одну из точек добавленных на этой итерации, то запишем в нее val+1, и уже не перепишется это значение?
In the last question, how do we know that when we take the log, we wont run into precision issues?
18210431 can anyone please explain why this solution passed problem D? Thanks in advance. why the first n + m points will be the best ones...
It isn't correct. Read this comment.
many thanks.
I use python on problem D,I try my best and finally got
TLEon test#48. Other people use python only pass test#19.Is python too slow to accept the problem D? my submission, use
BFS:18233710I have try many kind of constant optimization, so meet test#48, else will got TLE on earlier test. It looks that, I should not use python to do such problems, which have strict time limit.
now I use c++ accept, but I use 500ms , someone use 100ms , I think his program in python can accept, I will learn his program.
in problem D div2(Vanya and treasure), i don't understand why the complexity is n*m*sqrt(n*m), and also i don't understand why do we have 2 cases when cnt[color]·cnt[color - 1] ≥ n·m and the other, what's the idea behind that ?
to avoid TLE we have those 2 cases !
In problem D, someone solved it like this : First, iterating value v from 1 to p-1. For selected v, we can get positions which has value v (let's say these are in group i) and positions having value (v+1) (group j). when connecting these two groups, there can be a lot of connections if both are more than 10000, whatsoever. But sorting group i by using sum of distances from start and just seeing maximum 600 positions in group i(maxmimum(n+m)=600) may reduce time complexity. This solution is very fast, but I wonder if it can be ensured. (Of course this was accepted in system test) Can someone prove or disprove this solution?
I try to disprove this solution, if I correctly understood it. Assume there are values in matrix like this (i in [1..n], j in [1..m]): if i > 1 then value is equal to 1; if (i,j) == (1, m) then value is equal to 2; if (i,j) == (1, m-1) then value is equal to 1; if (i,j) == (1, 1) then value is equal to 4; else value is equal to 3. Then we need to take key with value 2 passing to first row. But by your algorithm we pass to only 600 nearest keys with value 1 and go necessarily to the second row (if n and m are big, for example equal to 300).
I wrote a solution for vanya and treasure (div2 D) using 2D sgement tree but i am getting TLE. i made it recursive not iterative like the tutorial does this cause TLE? i don't understand the tutorial implementation :/
Can someone tell me why this code is right?what dose 600 meaning in this code?I just thought this code is wrong.but I can't get a test to hack it.sad...If this code is right ,Can someone told me why?19380993
In problem 677E - Vanya and Balloons, I got WA and i can not find any bug in my solution, and i stressed it with more than 80k random tests and all of them got the correct output!!!
could anyone provide a counter-test.
Как минимум дважды спросили, как доказать в задаче D, что если у нас cnt[x] * cnt[x — 1] <= nm, то в сумме это уложится в асимптотику? Дважды спросили и дважды riadwaw доказал, почему у нас часть с бфс-ом уложится в асимптотику, но это не то, что просили доказать.
For problem 677D - Vanya and Treasure, if dp[x][y] is storing minimal distance from previous color, than for color 1, I think dp[x][y] = abs(x-1) + abs(y-1)..
the solution in editorial uses indexing from 0. so it is x+y :).