Число как сумма квадратов

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Приветствую всех! На днях я решал задачу, в которой требовалось определить, представимо ли число N < 10¹⁵ в виде суммы двух квадратов. И у меня возникли проблемы с этим, банальный перебор за корень давал TL. Так же пробовал разложить на простые сомножители за тот же корень, и потом проверял четность степеней у простых делителей вида 4k + 3, опять же TL. Скорее всего задача сдается за корень, и мне интересно именно техническая реализация этого, т.е. как конкретно писать аккуратный перебор или факторизацию за корень, и в чем конкретно проявляется эта аккуратность. Если что, эта задача с тимуса link HERE Заранее благодарен!

Комментарии (33)

Показать архивные | Написать комментарий?

Tranvick

13 лет назад, # |

← Rev. 2 →

+13

Заводим 2 указателя i и j. Изначально i = 1,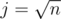 $\text{[math]}$ . На каждой итерации увеличиваем i на единицу, а j уменьшаем до тех пор, пока i² + j² > n. Когда-нибудь получится, что i² + j² = n. Либо не получится, если число непредставимо в виде суммы двух квадратов.

→ Ответить

13 лет назад, # ^ |

Вот кусок моего кода, который я сдавал где-то год назад:

bool two_square(ll x){
	ll i,j,en=(ll)(sqrt((double)x));
	for (i=1,j=en;i<=j;i++){
		while (i*i+j*j>x) --j;
		if (i*i+j*j==x) return 1;
	}
	return 0;
}

savinov

Большое спасибо!

riadwaw

Можно же просто завести 1 "указатель", а второй считать, просто идти не до n а до корня

Kostroma

тогда будет тратиться время на извлечение корня в double. Может получиться дольше, наверно)

Если я правильно понял, то на каждой итерации у вас будет вызываться функция sqrt. Такое решение невозможно сдать из-за TL, всё-таки извлечение корня — довольно трудоемкая операция.

Ок.

RomaWhite

У меня прошло и с sqrt. Код

Весело. Что-то я не подумал так ускорить. У меня было немного более "влоб" и падало по тайму где-то после 10ого теста.

goo.gl_SsAhv

корень не обязательно каждый раз извлекать, можно что-то возводить в квадрат, а можно воспользоваться тем что (x+1)^2 == x^2+2x+1 и каждый раз прибавлять/вычитать 2x+1

AlexFetisov

Вроде еще можно предпросчитать квадраты в хеш таблицу до 10^7, тогда непокрытых будет немного. Я как то так сдавал когда-то.

wil93

How can you use an algorithm that checks N = a²+b² in the problem you linked? It asks for the minimum number of squares that sum to N, am I right?

ibra

a little hint

http://en.wikipedia.org/wiki/Lagrange%27s_four-square_theorem

← Rev. 3 →

+10

Any natural number can be represented as the sum of four integer squares. We check that N = a². If not, we check that N = a² + b². If this is not correct, we check that N = a² + b² + c². And the answer is 4, if this is also not correct.

+14

how can we check if N can be represented as a sum of three squares fast?

niklasb

The following question on MathOverflow might help: http://mathoverflow.net/questions/57981/testing-whether-an-integer-is-the-sum-of-two-squares

EDIT: Sorry, I misread your comment :)

OSt

-15

IMHO, in that problem more easy to check if N can be represented as sum of 1,2,4 squares. Else — 3. :-)

afix

27 = 1*1 + 1*1 + 3*3 + 4*4 = 1*1 + 1*1 + 5*5
27 != a*a
27 != a*a + b*b
Fail.

if N != (8*t+7)*4^k then there are 3 squares.

oh, don't you know the proof or some link with the proof?

And now read your previos explanation.

-8

sorry, I've misunderstood you

int three_square(ll x){
	while (!(x&3)) x>>=2;
	return (x+1)%8;
}

It returns 0, if x is not a sum of three squares.

CherryTree

How come?

This is a very difficult method of pen and paper :)

I think that algorithm follows this: http://www.proofwiki.org/wiki/Integer_as_Sum_of_Three_Squares

jaineshp

9 лет назад, # ^ |

-12

For sum of two squares, how can it be modified?

ha1vanka

+29

Don't answer him. This is one of the problems from a running contest.

-14

Sorry?

I_will_win_a_div1_round

-27

Motori

red_coder

according to me we can run a loop in which 'i' goes from 1 to sqrt(N/2) and if N-i*i is a perfect square we are done....

for(int i=1; i*i<=N/2; i++) { if((N-i*i) is a perfect square) done; }

its complexity is O(sqrt(N)).....

How do you check number for square? I did the same and used sqrt() and got TL.

Oi.

An arbitrary positive number n is expressible as the sum of two squares iff, given its prime factorization

n=p1^(a1)p2^(a2)p3^(a3)...pk^(ak),

none of pi^(ai) +1 is divisible by 4 (Conway and Guy 1996, p. 147). http://mathworld.wolfram.com/SquareNumber.html

Блог пользователя savinov