http://www.ioi-jp.org/apio2012/ — asian pacific informatics olympiad. Был утренний тур, который недавно закончился, но будет еще второй, такой же, вечером. Предлагаю после него обсудить задачи.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
27:46:56
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
27:46:56
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 13:48:06 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Продолжительность тура — 5 часов. Начало в семь по Москве. Есть условия на английском, на русском —
нетсм. условия для Казахстана. Оценка по подгруппам тестов. Естьполныйфидбэк (без токенов, неограниченное количество попыток) вида "вердикт на каждом тесте" — время выполнения/память/информация о полученных баллах и группах тестов отсутствует.Рекомендую поучаствовать — мне понравилось.
У нас были условия на русском (для Казахстана). И разве там полный фидбек?
Действительно, для Казахстана условия на русском.
Мне почему-то казалось, что да. Сейчас посмотрел еще раз — тестов стало сильно больше, значит, нет. Что-то я всё-таки мало спал.
и вроде тесты различаются от старых
1) сколько задач?
2) можно ссылку на прошедший контест (на условия хотя бы)?
А вы не хотите вечером поучаствовать? Условия мне стали недоступны, равно как и полные результаты тестирования.
вечером будет на тех же задачах?
Да, соревнование было в один день и во все предыдущие года было 3 задачи.
Я что-то не пойму куда там тыкать, чтобы поучаствовать?
Слева Competition -> Open contest. Там есть ссылка: http://open.apio2012.ioi-jp.org/.
Да, спасибо. А у меня одного на этом сайте иногда какие-то иероглифы высвечиваются и все жестоко тормозит?
Не знаю, у меня вроде все нормально.
правильно я понимаю, что от времени сдачи и количества посылок не зависит?
Да, правильно, это же IOI система.
UPD: упс, ошибся.
Вот блин, так и не додебажил 3ю. Оказывается, там еще и группы тестов при проверке.
Да, даже в правилах написано. А как время считается, есть идеи? Похоже на ACM.
Наверное стоило прочитать правила :) Тогда бы хоть частичное решение по последней написал, а то видел что какие-то АС есть и решил что они и будут в финальном скоре.
А время там берется последнего увеличения баллов, видимо.
UPD: Не, туплю, время явно не такое берется.
Крутые у них компы — по 3-й квадрат запихался. У меня помимо бага из-за которого ВА еще был прокол в идее из-за которого оно ТЛило. Исправлять уже было лень, так я немного соптимизировал константу и оно прошло. Локально на худшем тесте посчитал количество итераций — выходит квадрат деленный на небольшую константу.
А за сколько зашло? Может, тесты кривые?
Зашло за 2.3.
Сколько работает на таком тесте:
Проведём главную диагональ в квадрате, верхнюю половину утыкаем стрелочками вправо, нижнюю — стрелочками вверх.
Он ломает только так мой лучший квадрат.
Ну я тестил на аналогичном тесте: в одной строке слева стрелочки вправо, а справа от них в этой же строке стрелочки влево, причем все расположено симметрично относительно центра строки. Локально работает 3980 и выполняет 2.5 миллиарда операций.
А расскажите, пожалуйста, как решать B и С.
И ещё расскажите, как А на полный балл делать.
Я делал немного по-извращенски: Посчитаем для всех вершин отрезки входа-выхода. Тогда задача свелась к следующей: на отрезке находить максимальное кол-во элементов, которое можно взять, чтобы сумма не превысила M. Для этого отсортируем все вершины по возрастанию ci и будем в порядке сортировки добавлять в персистентное ДО, которое будет считать сумму на отрезке и кол-во не нулей. Теперь, чтобы решить исходную задачу можно сделать бинпоиск по версии ДО и найти самую позднюю (т.е. с максимальным кол-вом добавленных элементов) версию, такую, что в ней сумма на отрезке не превышает M. Получается nlog2n. К сожалению, без оптимизаций такое не заходило.
Еще можно за ту же асимптотику, но по-другому. Просто в dfs-е можно было поддерживать для вершины декартово дерево ci ее потомков. Если сливать декартовы деревья детей, добавляя элементы меньшего в большее, несложно доказать, что в сумме мы сделаем nlog2n операций. Узнавать наибольшее кол-во с допустимой суммой можно простым спуском по дереву.
Вместо декартового дерева можно просто хранить priority queue из STL. Всего выходит около 50 строк кода
priority_queue же умеет только добавлять и извлекать максимум? Как быстро считать сумму?
Мы будем отдельно хранить для каждой кучи сумму элементов в ней. Тогда когда сливаем две кучи просто складываем эти значения. Когда мы будем обрабатывать текущую вершину, сольем все кучи ее детей в одну + Ci текущей вершины. Потом будем выкидывать наибольший элемент кучи, пока сумма всех ее элементов больше чем M. При это несложно поддерживать сумму кучи.
Точно, у нас же M одно на тест.
Я кодил за ту же асимптотику, но можно и за O(NlogN). Вместо каких-либо деревьев можно хранить отсортированные векторы и мерджить их при подъеме по дереву.
А почему будет O(NlogN)? Вроде каждая вершина может просматриваться много раз.
Да, это я глупость сказал. Но зато, если использовать какую-нибудь такую кучу вместо priority_queue, то сливать сможем за O(logN) и в сумме будет O(NlogN).
а за O(Nlog^2N) ты как делал?
Просто при подъеме по дереву сливал priority_queue. Если сумма всех элементов в куче больше M, то доставал максимальный до тех пор, пока она не станет меньше.
А опять — разве каждая вершина не будет рассматриваться много раз?
А как именно сливать очереди?
Чтобы слить 2 очереди, мы из меньшей перебросим по одному все элементы в большую. Нетрудно заметить, что каждый элемент будет перекочевывать O(logN) раз.
Да, понял, спасибо.
A вроде как можно сделать и за (я не писал). Идея такая же, как и тут (k-я порядковая статистика на отрезке за
(я не писал). Идея такая же, как и тут (k-я порядковая статистика на отрезке за  онлайн персистентным деревом), только в персистентном дереве мы еще будем дополнительно хранить сумму соответствующих элементов, тогда спускаться будем так, чтобы сумма была ≤ M.
онлайн персистентным деревом), только в персистентном дереве мы еще будем дополнительно хранить сумму соответствующих элементов, тогда спускаться будем так, чтобы сумма была ≤ M.
Задача B:
Теперь необходимое условие: размер максимального подмножества попарно непересекающихся отрезков не превосходит k и у нас не менее k свободных мест. Очевидно, что если это не так, то мы не сможем выбрать k кустов и покрыть все отрезки. Докажем, это этого достаточно. Существует известный жадник для поиска такого подмножества — отсортировали отрезки по правому концу и набрали совсем жадно. Теперь выберем в качестве кустов правые концы этих отрезков. От противного несложно показать, что все отрезки покроются (иначе мы на каком-то шаге могли взять строго лучший отрезок). Если отрезков меньше k, то можно взять еще любые кусты.
Таким образом, умеем за O(n) проверять непротиворечивость, если запретить еще один куст (сортировка идёт прекалком).
Итоговое время работы — .
.
Можно за линию. Оно все сводится к системе разностных ограничений, граф которой имеет очень частный вид. В нем кратчайшие пути можно за линию предпосчитать и за константу проверять для каждого куста.
А к чему там кратчайшие пути в графе? Я правильно понимаю, что вершина — это промежуток между кустами, а ребро — сколько на заданном отрезке сидит ниндзя?
К системе разностных ограничений задачу можно свести так. Поставим в каждой ячейке 1, если там сидит ниндзя и 0, если не сидит. Перейдем к массиву частичных сумм (назовем его A) в который добавим еще фиктивную ячейку с номером 0, в которой никто не сидит. Тогда задача поиска расстановки ниндзя эквивалентна следующей системе линейных ограничений:
Построим граф, в котором вершинам будут соответствовать Ai, а ребрам — ограничения. Для каждого ограничения вида Ai - Aj ≤ x проведем ориентированное ребро из j в i веса x.
Есть теорема, что система разностных ограничений имеет решение тогда и только тогда, когда в этом графе нет отрицательного цикла. По условию существует хотя бы одна расстановка ниндзя, так что изначально отрицательных циклов в нем нет.
Теперь мы хотим проверить, есть ли расстановка в которой никто не сидит в кусте i. Для этого мы заменим ограничение Ai - Ai - 1 ≤ 1 на Ai - Ai - 1 ≤ 0 и проверим, не образовался ли отрицательный цикл в графе. Рассмотрим 2 случая:
Да, это и имел ввиду. Про теорему не знал, спасибо. А там еще что-нибудь полезное есть?
Из того что я знаю — это еще нахождение решения в случае его существования. Для этого нужно запустить поиск кратчайшего пути одновременно от всех вершин, проинициализировав расстояние нулями. Полученные расстояния в конце и будут искомым решением. После этого можно их все одновременно двигать на одну и ту же константу, чтобы загнать в нужные рамки.
Свойством найденного таким образом решения (без прибавления константы) является максимальность суммы xi при условии, что xi ≤ 0 для всех i.
Еще одним свойством этого же решения является минимальность разности между максимальным и минимальным значениями xi.
Так можно же подсчетом сортировать отрезки, разве нет? Ведь если у нас будет два отрезка с одной правой координатой, то можно оставить только один, который короче. Тогда тоже получится O(n).
Можно, но мне легче написать
sort, благо ограничения позволяют.C:
O(n2). Научимся считать для каждого ножа, сколько он пролетит. Поймём, что пока никто ни с кем не столкнулся, ничего принципиально не меняется. Возможных столкновений — O(n2). Переберём все пары, посчитаем за O(1), столкнутся ли два ножа, если да, то когда, отсортируем события, пробежимся по ним. Берём все события в текущей момент, оба ножа из которых еще живы, убиваем их. Получили, сколько пролетел каждый нож. Теперь задача: есть куча отрезков, сколько они закрасили клеток? Это какой-то scanline с деревом отрезков. Т.е. .
.
Поймём, что все события нам рассматривать не нужно. Сделаем так: цикл, пока живы все ножи. Первым действием будет получить самые ближайшие события. Вторым — их обработка. Заметим, что два ножа могут столкнуться, только если они лежат на одной вертикали/горизонтали/диагонали. Теперь, чтобы обработать только самое ближайшее событие, для каждого ножа нам не нужно рассматривать все остальные — только соседей по направлениям (но не просто ближайших, а ближайших, которые смотрят в нужную сторону). Таким образом, мы за умеем находить все ближайшие события. Выполним все события, которые произойдут раньше всех (например, в момент t). Заметим, что поменялось немного — исчезли какие-то ножи. Теперь на следующей итерации нам бессмысленно обновлять информацию для ножей, все соседи которых остались живы. Нам требуется обновить информацию только дя O(X) ножей. где X — количество обработанных событий. Таким образом, мы выполним
умеем находить все ближайшие события. Выполним все события, которые произойдут раньше всех (например, в момент t). Заметим, что поменялось немного — исчезли какие-то ножи. Теперь на следующей итерации нам бессмысленно обновлять информацию для ножей, все соседи которых остались живы. Нам требуется обновить информацию только дя O(X) ножей. где X — количество обработанных событий. Таким образом, мы выполним  предподсчёта, потом на каждой итерации еще
предподсчёта, потом на каждой итерации еще 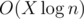 . В сумме у нас не более O(n) событий (каждое событие убивает хотя бы один нож, но, например, четыре ножа могут столкнуться в одной точке и это будет 6 событий, но это максимум). Поэтому итоговое время работы
. В сумме у нас не более O(n) событий (каждое событие убивает хотя бы один нож, но, например, четыре ножа могут столкнуться в одной точке и это будет 6 событий, но это максимум). Поэтому итоговое время работы  . События можно хранить в
. События можно хранить в
priority_queue, удалять нам необязательно.Is there a way to solve kunai without using 8 range trees?