Разбор задач Educational Codeforces Round 13

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	156
8	TheScrasse	154
9	Dominater069	153
9	nor	153

678A - Вася любит числа

Задачу предложил Әбдірахман Исмаил bash.

Нам нужно найти минимальное x, что x * k > n. Легко видеть, что 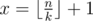$\text{[math]}$ . Для подробного знакомства с математическими функциями пола и потолка я рекомендую книгу авторов Грэхем, Кнут, Паташник "Конкретная математика". В этой книге есть отдельная глава, посвящённая этим функциям и их свойствам.

Решение на С++

li n, k;

bool read() {
	return !!(cin >> n >> k);
}

void solve() {
	cout << (n / k + 1) * k << endl;
}

Сложность: O(1).

678B - Такой же календарь

Задачу предложил Артур Яворски KingArthur.

Два календаря совпадают если и только, если в них одинаковое количество дней и они начинаются с одного дня недели. Таким образом, достаточно было просто перебрать следующий год, поддерживая первый день недели в году. На самом деле день недели каждый год увеличивается на единицу. Исключением являются високосные годы, когда день недели увеличивается на два.

Решение на C++

int y;

bool read() {
	return !!(cin >> y);
}

bool leap(int y) {
	return y % 400 == 0 || (y % 4 == 0 && y % 100 != 0);
}

void solve() {
	bool is_leap = leap(y);
	int d = 0;
	do {
		d++;
		if (leap(y)) d++;
		y++;
		d %= 7;
	} while (d || leap(y) != is_leap);
	cout << y << endl;
}

Сложность: O(1) — легко видеть, что количество итерация не превосходит небольшой константы.

678C - Мила и шоколад

Задачу предложил Sheikh Monir skmonir.

Легко видеть, что в оба цвета мы можем покрасить доски с номерами кратными lcm(a, b) — НОК чисел a и b. Очевидно, что эти доски выгоднее красить в более дорогой цвет. Таким образом, ответ равен: 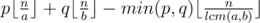$\text{[math]}$ .

Решение на C++

li n, a, b, p, q;

bool read() {
	return !!(cin >> n >> a >> b >> p >> q);
}

li gcd(li a, li b) { return !a ? b : gcd(b % a, a); }
li lcm(li a, li b) { return a / gcd(a, b) * b; }

void solve() {
	li ans = 0;
	ans += (n / a) * p;
	ans += (n / b) * q;
	ans -= (n / lcm(a, b)) * min(p, q);
	cout << ans << endl;
}

Сложность: O(log(max(a, b))).

678D - Итерированная линейная функция

Задачу предложил Zi Song Yeoh zscoder.

В этой задаче можно было вывести формулу в качестве ответа: для этого нужно было посчитать сумму геометрической прогрессии. Далее формулу было легко посчитать с помощью бинарного возведения в степень.

Я опишу более сложное, но более общее решение. Если у нас есть некоторый набор переменных, который пошагово пересчитывается друг через друга с помощью линейной функции, то можно применить бинарное возведение в степень матрицы. Итак, в нашей задаче переменная была одна x. Новая переменная x' получалась по формуле A·x + B. Рассмотрим матрицу z = [[A, B], [0, 1]] и вектор v = [x, 1]. Умножим z на v слева. Легко видеть, что получится вектор v' = [x', 1]. Таким образом, чтобы сделать n итераций, мы просто должны n раз умножить слева матрицу z на вектор v. В силу свойства ассоциативности операции умножения матриц перемножение мы можем сделать бинарно.

В качестве упражнения можете попробовать выписать самостоятельно матрицу для чисел Фиббоначи и научиться их быстро считать. Под спойлером матрица и вектор.

Матрица и вектор для чисел Фиббоначи

Решение на C++

int A, B, x;
li n;

bool read() {
	return !!(cin >> A >> B >> n >> x);
}

const int mod = 1000 * 1000 * 1000 + 7;

inline int add(int a, int b) { return a + b >= mod ? a + b - mod : a + b; }
inline int mul(int a, int b) { return int(a * 1ll * b % mod); }
inline void inc(int& a, int b) { a = add(a, b); }

void mul(int a[2][2], int b[2][2]) {
	static int res[2][2];
	forn(i, 2)
		forn(j, 2) {
			res[i][j] = 0;
			forn(k, 2) inc(res[i][j], mul(a[i][k], b[k][j]));
		}
	forn(i, 2) forn(j, 2) a[i][j] = res[i][j];
}

void bin_pow(int a[2][2], li b) {
	static int res[2][2];
	forn(i, 2) forn(j, 2) res[i][j] = i == j;

	while (b) {
		if (b & 1) mul(res, a);
		mul(a, a);
		b >>= 1;
	}

	forn(i, 2) forn(j, 2) a[i][j] = res[i][j];
}

void solve() {
	int z[2][2] = {
		{ A, B },
		{ 0, 1 }
	};
	bin_pow(z, n);
	int result = add(mul(z[0][0], x), z[0][1]);
	cout << result << endl;
}

Сложность: O(logn).

678E - Очередной турнир ситхов

Задачу предложил и подготовил Алексей Дергунов dalex.

Давайте решать задачу динамикой. z_mask, i — наибольшая вероятность выиграть Ивану, если джедаи из маски mask уже хоть раз сражались, а в живых остался только i-й джедай. Для подсчёта динамики переберём следующего джедая (ему придётся сражаться против i-го джедая): 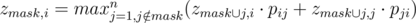$\text{[math]}$ .

Решение на C++

const int N = 20, EXPN = (1 << 18) + 3;

int n;
ld p[N][N];

bool read() {
	if (!(cin >> n)) return false;
	forn(i, n) forn(j, n) assert(cin >> p[i][j]);
	return true;
}

ld z[EXPN][N];

ld solve(int mask, int i) {
	ld& ans = z[mask][i];
	if (ans > -0.5) return ans;
	if (mask == (1 << n) - 1) return ans = !i;
	ans = 0;
	forn(j, n)
		if (!(mask & (1 << j))) {
			ld cur = 0;
			cur += solve(mask | (1 << j), i) * p[i][j];
			cur += solve(mask | (1 << j), j) * p[j][i];
			ans = max(ans, cur);
		}
	return ans;
}

void solve() {
	if (n == 1) {
		puts("1");
		return;
	}

	forn(i, 1 << n) forn(j, n) z[i][j] = -1;

	ld ans = 0;
	forn(i, n)
		forn(j, i) {
			int mask = (1 << i) | (1 << j);
			ld cur = 0;
			cur += solve(mask, i) * p[i][j];
			cur += solve(mask, j) * p[j][i];
			ans = max(ans, cur);
		}
	cout << ans << endl;
}

Сложность по времени: O(2ⁿn²).

Сложность по памяти: O(2ⁿn).

678F - Лена и запросы

Задачу предложил AmirMohammad Dehghan PrinceOfPersia.

Посмотрим на задачу геометрически: пары чисел в множестве это просто прямые, задача по вертикальной прямой найти самое верхнее её пересечение с какой-либо прямой.

Разобьём все запросы на $\text{[math]}$ блоков. Рассмотрим те прямые, которые были добавлены до начала блока и не будут удалены в нём. Построим по этому множеству нижнее огибающее множество. Теперь, чтобы ответить на один запрос третьего типа нужно взять максимум по прямым нижнего огибающего множества и по запросам в блоке до текущего запроса. Последних не более $\text{[math]}$ , поэтому по ним мы можем пройти в лоб и обновить ответ. Теперь посмотрим на все запросы в блоке третьего типа, отсортируем их слева направо и будет искать оптимальную прямую в огибающем множестве с помощью двух указателей.

Решение на C++

const int N = 300300;

int n;
int t[N], a[N], b[N], id[N], q[N];

bool read() {
	if (!(cin >> n)) return false;
	forn(i, n) {
		assert(scanf("%d", &t[i]) == 1);
		if (t[i] == 1) {
			assert(scanf("%d%d", &a[i], &b[i]) == 2);
		} else if (t[i] == 2) {
			assert(scanf("%d", &id[i]) == 1);
			id[i]--;
		} else if (t[i] == 3) {
			assert(scanf("%d", &q[i]) == 1);
		} else throw;
	}
	return true;
}

bool in_set[N], deleted[N];
vector<pair<pti, int>> lines;
vector<pti> envelope;

void build_envelope() {
	envelope.clear();
	envelope.reserve(n);

	forn(ii, sz(lines)) {
		int i = lines[ii].y;
		if (in_set[i] && !deleted[i]) {
			assert(t[i] == 1);
			pti c(a[i], b[i]);
			while (!envelope.empty()) {
				pti b = envelope.back();
				if (b.x == c.x) {
					envelope.pop_back();
					continue;
				} else if (sz(envelope) > 1) {
					pti a = envelope[sz(envelope) - 2];

					ld xc = ld(c.y - a.y) / (a.x - c.x);
					ld xb = ld(b.y - a.y) / (a.x - b.x);

					if (xc < xb) {
						envelope.pop_back();
						continue;
					}
				}
				break;
			}
			envelope.pb(c);
		}
	}
}

li ans[N];
vector<pti> qs;

void process_qs() {
	sort(all(qs));

	int p = 0;
	forn(i, sz(qs)) {
		li q = qs[i].x;
		int id = qs[i].y;

		while (p + 1 < sz(envelope)) {
			li cval = envelope[p].x * q + envelope[p].y;
			li nval = envelope[p + 1].x * q + envelope[p + 1].y;
			if (cval > nval) break;
			p++;
		}

		if (p < sz(envelope)) {
			ans[id] = envelope[p].x * q + envelope[p].y;
		}
	}
}

void solve() {
	lines.clear();
	lines.reserve(n);
	forn(i, n) if (t[i] == 1) lines.pb(mp(mp(a[i], b[i]), i));
	sort(all(lines));

	memset(in_set, false, sizeof(in_set));
	memset(deleted, false, sizeof(deleted));
	forn(i, n) ans[i] = LLONG_MIN;

	int blen = int(sqrtl(n));
	blen = 2500;
	for (int l = 0; l < n; l += blen) {
		int r = min(n, l + blen);

		memset(deleted, false, sizeof(deleted));
		fore(i, l, r) if (t[i] == 2) deleted[id[i]] = true;
		build_envelope();

		qs.clear();
		qs.reserve(r - l);
		fore(i, l, r) if (t[i] == 3) qs.pb(mp(q[i], i));
		process_qs();

		fore(i, l, r) {
			if (t[i] == 1) in_set[i] = true;
			else if (t[i] == 2) in_set[id[i]] = false;
			else {
				fore(j, l, r) {
					if (t[j] == 1 && in_set[j])
						ans[i] = max(ans[i], li(a[j]) * q[i] + b[j]);
					else if (t[j] == 2 && in_set[id[j]])
						ans[i] = max(ans[i], li(a[id[j]]) * q[i] + b[id[j]]);
				}
				if (ans[i] != LLONG_MIN) printf("%lldn", ans[i]);
				else puts("EMPTY SET");
			}
		}
	}
}

Сложность: 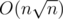$\text{[math]}$ .

Комментарии (42)

Показать архивные | Написать комментарий?

Ishan.nitj

8 лет назад, # |

+17

Please write the editorial for E

→ Ответить

Um_nik

+13

В C же O(logC).

Edvard

8 лет назад, # ^ |

Да, конечно. Поправил.

ffao

+32

About problem E:

After some interesting discussion, I was wondering what exactly can we say about the optimal solution?

Let's assume that optimal sequence can be represented by a sequence a₁, a₂, ..., a_n of fighters in which a₁ fights a₂, then the winner fights a₃, etc. Intuitively, the probability someone wins is higher the more to the right of the sequence it is: this implies a_n should be Ivan in an optimal sequence.

Now who do we want at the second to last position? That person will be given a greater chance to fight Ivan, so we want it to be the one that has the smallest chance to win against him.

Generalizing to all n players, we have the following O(n²) greedy solution: construct the sequence of fighters from the last to the first. For each pick, pick the available fighter that makes probability of Ivan winning in current sequence highest possible.

Code: 18489412

Of course, there's no such thing as "proof by AC", so I'm still curious if this solution is actually correct. If it is, I think it is quite interesting :)

dalex

Some history: the setting was taken from Timus 1218. In 1218, we discovered a NlogN solution and included that problem into our contest at Petrozavodsk camp, where 7 teams out of 50 solved it.

As my teammates just said, it became a tradition: all "Jedi Tournament" problems can be solved better than author initially thought. You could have done the same with your solution.

Actually I've discussed with dalex that. And I thought about the same thing. But both of us agreed that greedy solution is incorrect here.

+11

If you discussed this before the contest, shouldn't you have included a test that fails the greedy solution?

I'm also curious to know how you reached this conclusion.

+10

I thought about different greedy solution. This one passes random tests and must be correct.

Oh you misunderstood. We have not a countertest, we just thought that greedy solution is incorrect.

Avitella

← Rev. 2 →

Почему в E что-то вообще умножается на p_ji? Это же подразумевает, что побеждает джедай j, а пересчитываем мы для побеждающего i.

MuratKhayrulin

В данной формулировке интересно не то, как состояние достигнуто, а то, какая наибольшая вероятность может быть получена из этого состояния. То есть в правой части выражения перебираются следующие бои и учитываются оба исхода каждого боя.

adkroxx

Another solution for problem F in O(N*log²N).

AFatWolf

Could u please go for more detail about it?? I have difficulty in reading and understanding ur code :P

Explained.

Do you use the technique with storing the blocks of the sizes 2^k?

Problem to find the topmost intersection of the vertical line with the lines from the set can be solved with Convex Hull Trick.

I builded a segment tree of CHT over time interval.
For i^th insertion query update the segment tree with this line in range [ i, time till i^th line exists ].
For every query of 3rd type it is equivalent to point query at that point of time.

Nice. But I think it's more complicated.

During contest I tried with the same approach as mentioned in editorial (Submission). But it timed out because my complexity was O(N^1.5 * logN). So I had to go this way but it seems that logN factor can be removed.

mnaeraxr

I solved the problem using your idea but with complexity O(N*logN). Submission here: 18842789

Insertion in logN nodes is log²N, right ?

P.S: Your N*logN is slower than mine N*log²N.

jcg

← Rev. 4 →

Actually if you insert the lines in sorted order the overall complexity for insertion is $\text{[math]}$ because you insert in $\text{[math]}$ nodes in total linear time. This was mnaeraxr and I did (using your idea, btw) 18845711. You probably didn't look deeper into mnaeraxr code.

wineColoredDays

Can anyone explain a little more about the recurrence relation in E?

renadeen

http://codeforces.net/blog/entry/45405?#comment-310782

s17b2_voroneckij

Почему код решений такой плохой?

А что именно плохо? Если вопрос в дефайнах или в сокращениях типа ld вместо long double, то в олимпиадном сообществе очень многие используют их.

Ну да, из-за них читать неудобно.

voroniy

И вообще, ваш код — отстой

deep9539

Can someone explain the editorials for Problem E in a somewhat detail manner, it would be a great help.

My approach. First observe that our jedi should fight last. Then we exclude him from the set of siths. Let mask be some subset of set of siths (without jedi) and i is a sith of this subset. Then dp[mask, i] is maximum (among all sequences of siths) conditional probability that Ivan wins tournament given that siths from mask already fought and i-th is a winner.

We init our dp with full mask:

for (int i = 1; i < n; i++)
    dp[all, i] = p[0, i];

where all is full mask. That means, if all siths already fought and i-th is a winner then probability that Ivan wins tournament is equal to probability of win this sith. Then we loop over smaller and smaller mask's and calculating their values from previous calculations. To find dp[mask, i] use formula from editorial. Should be more clear now. If not I can explain in more detail.

And the end answer will be maximum of dp[mask_i, i]. It is conditional probability that Ivan wins tournament given that i-th sith is the first participant in tournament.

HynDuf

5 лет назад, # ^ |

Could you explain more about the formula. I want to ask some specific questions:

z(mask,i) is when the i-th wins so why do they + z(mask U j,j)*p[j][i] as well.
z(mask,i) is the "maximal probability of Ivans victory if the siths from the mask already fought and the i-th sith left alive". So is Ivans necessarily be i or some bit 1 in mask or some other siths?

This contest has been so long but if you could answer these, I would be really thankful. I have comtemplating about this problems for a week but still didn't figure it out. Thanks <3

Mohamed_Ayman

here editorial of 678D — Iterated Linear Function for any one need to read it.
http://codeforces.net/blog/entry/45413

manjunath1996

Please ,explain me the solution of Another Sith tournament.Please explain me in words how that formula comes??

letsbe

In above code for problem F, I want to know why blen is 2500, not sqrt(n). Please tell me.. my submission also TLE when i set blen sqrt(n), but accept when i set blen 2500. sorry for my fool english

__important__

we need sorting all query in each block. so complexity is O(N * N / size + N * log2(size) + size * size). for best we choose size = 2500.

akshit.lite

Can someone explain how is the complexity of solution of Problem E , in the editorial O(N^2 * 2^N) ? I think it is O(N^3 * 2^N) as for every O(n^2) starting pairs we have an O(n) loop to set the next winner.

DeerInForestovo

5 лет назад, # |

Problem F 线段树分治+斜率优化可以做到O(NlogN)吧

Could you explain more about the formula in problem E. I want to ask some specific questions:

roll_no_1

$$$z(mask, i)$$$ is not the probability that the $$$i$$$-th sith wins. Remember that we are calculating the probability of the $$$0$$$-th sith being the ultimate winner. It simply says that all siths in the mask have fought some match and the only sith alive out of those currently is the $$$i$$$-th sith.
Ivan corresponds to the $$$0$$$th bit. There are $$$2$$$ cases:
$$$1$$$. $$$0$$$-th bit is $$$0$$$, which means Ivan hasn't fought yet.
$$$2$$$. $$$0$$$-th bit is $$$1$$$. In this case, if $$$i \ne 0$$$, this means that Ivans fought but was killed. So, the answer for this state is $$$0$$$. Otherwise, Ivan is the survivor from all matches conducted so far and we proceed with the tournament.

spookywooky

678D - Iterated Linear Function How do we come from knowing that we have to find a matrix to the actual matrix? And what about the vector v, where that comes from?

coder_dtu_17

Here is a simple mathematical approach:

After simplifying:

gn(x) = (a^n)*x + b*( 1 + a + a^2 + a^3 ....... a^(n-1) )

[ 1 + a + a^2 + a^3 ....... a^(n-1) ] forms a Geometric Progression, whose sum can be calculated as:

S = b* (a^n-1)/(a-1)

for the solution, see my submission 78952460

sigma_g

4 года назад, # |

My solution to Sith Tournament (problem E) works without an extra index in DP. It is slightly different from the editorial.

Mask of (n — 1) bits represents which siths are still alive (as ivan will always stay alive, no need for keeping an extra bit for him). dp[mask] represents probability Ivan wins given that the siths in mask are alive. dp[0] is trivially 1 (as mask=0 means all other siths have died). We compute dp in increasing value of mask.

For computing value of dp[mask], we simulate the situation where Ivan has to choose two siths for a fight, and where one of them dies. We just run a loop through all pairs of distinct set bits (b1 and b2), and update our dp as follows:

probA = beats[b1][b2] * dp[mask ^ (1 << b2)]; // b1 beats b2
probB = beats[b2][b1] * dp[mask ^ (1 << b1)]; // b2 beats b1
totalProb = probA + probB;
dp[mask] = max(dp[mask], totalProb);

Before exiting, we also pair each sith with Ivan himself, updating our dp[mask] as follows:

dp[mask] = max(dp[mask], beats[1][bit] * dp[mask ^ (1 << bit)]

In the end, we print dp[(1 << (n - 1)) - 1].

AC Submission

Блог пользователя Edvard

678A - Вася любит числа

678B - Такой же календарь

678C - Мила и шоколад

678D - Итерированная линейная функция

678E - Очередной турнир ситхов

678F - Лена и запросы