Hi everyone! I can't solve this problem, can you help me please?
Statement:
Given a list of words, you have to find an order in which a word A can be before to word B only if the last letter of A is the same that the first letter of B. This order must be circular, like this:
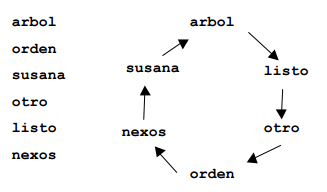
(LEFT: Given words. RIGHT: A possible ordering of the words)
Input: First line, the quantity of words N (1 <= N <= 9000). Next N lines have the words (one word per line). Lenght of each word don't exceed 6:
6
arbol
orden
susana
otro
listo
nexos
Output: If it's possible to make the circular ordering, print N lines with the words ordered (as the ordering is circular, you can start listing them with any word). If it's impossible, print "Impossible"
susana
arbol
listo
otro
orden
nexos
The first thing I know is that for finding the ordering you only need two letters (first and last of each word). I was thinking in Hamiltonian Cycle, but the input is too big.











Hint: it is hard to find a Hamiltonian cycle but easy to find Eulerian cycle. So, construct a graph so that you have to do the latter.
I'll try that. Thanks!
Construct a graph such that a->b exist if last character of a is same as first character of b .try finding a cycle of length N
I think it's almost like this problem.
You can find many solutions on google, like this one.
Yeah, it's very similar! Nice one!