Подсчёт количества масок среди данных, являющихся подмаской m, для всех m -- почему это работает?

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

На олимпиаде Казахстана прошлого года была задача "Количество совместимых чисел", которая сводится к такой: даны 22-битные маски a₁, a₂, ..., a_n (n < 10⁶), нужно посчитать d[m] — количество таких i, что a[i] является подмаской m (т.е. a[i] & m == a[i]).

Официальное решение решает эту задачу так:

for (int i = 0; i < n; i++) {
	d[a[i]]++;
}

for (int i = 0; i < 22; i++) {
	for (int mask = 0; mask < (1 << 22); mask++) {
		if ((mask & (1 << i)) == 0) {
			d[mask | (1 << i)] += d[mask];
		}
	}
}

Пытаясь решить эту задачу самостоятельно, я дошёл до этой идеи, но сразу отбросил, потому что мне показалось очевидным, что она какие-нибудь подмаски будет считать несколько раз. Сейчас я вроде бы почти убедил себя, что этого не происходит, но у всё ещё меня нет интуитивного понимания того, почему это должно работать. Может, это какой-то известный трюк, которого я не знаю? Или может просто кто-нибудь может объяснить логику этого подхода?

Спасибо!

Комментарии (10)

Написать комментарий?

Gassa

8 лет назад, # |

Можно сказать, что дело в порядке циклов.

Пусть мы хотим получить маску s. Рассмотрим её биты по порядку (внешний цикл по i). Для каждого бита i, если он единица, сделаем переход d[mask | (1 << i)] += d[mask];. Если он ноль, переход не происходит. Например, маска 13 (двоичная запись 1101) получается единственным способом:

при i = 0 по переходу d[1] += d[0],
при i = 2 по переходу d[5] += d[1],
при i = 3 по переходу d[13] += d[5].

Если бы порядок циклов был другим — внешний по mask и внутренний по i — действительно, каждая маска с x единичными битами получилась бы x! способами: биты могли добавиться в любом порядке.

→ Ответить

popoffka

8 лет назад, # ^ |

Что именно значит «маска 13 получается единственным способом»? Ведь, например, при i = 0, выполняется также и d[13] += d[12]

UnknownNooby

Имелось в виду, что у каждой маски ровно один путь, по которому она может пройти к конкретной надмаске, насколько я понял. Кажется, именно это мы и хотим доказать.

Да, я непонятно написал. Имелся в виду путь из 0 в 13. То есть в терминах задачи — пусть массив a состоит из одного нуля, и мы хотим ответ для m = 13.

Так вот, когда происходит d[13] += d[12];, в d[12] ещё ничего нет. Единица из d[0] в d[13] попадает единственным способом — как указано выше в комментарии.

В более общем случае — если x & y = x, то из y получается из x ровно одним способом. Рассмотрим те биты, в которых у x ноль, а у y единица. Переходы — прибавления этих битов в порядке возрастания их номеров.

Для визуализации можно нарисовать куб (вершины — числа от 0 до 7, соответствующие маскам от 000 до 111). Пусть рёбра по оси Ox красные и соответствуют прибавлению 1, по оси Oy синие и соответствуют прибавлению 2, по оси Oz зелёные и соответствуют прибавлению 4. На такой картинке можно посмотреть, сколько способов попасть из одной вершины в другую, если сначала можно идти только по красным рёбрам (i = 0 во внешнем цикле), потом только по синим (i = 1) и в конце только по зелёным (i = 2).

ilyakor

Можно посмотреть на это с другой стороны. Пусть d_i, mask — сумма по всем mask', таким что по первым i битам mask' — подмаска mask, а по остальным — в точности mask. Тогда d_0, mask — input задачи. Как перейти от i к i + 1? Если mask[i] = 0, то d_{i + 1, mask} = d_i, mask. Иначе, mask'[i] либо 1 (d_i, mask), либо 0 (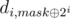 $\text{[math]}$ ).

В таком виде динамика более или менее очевидна, а то, что указано в посте, — просто оптимизированная версия, хранящая только один слой.

О, спасибо! Теперь мне более-менее понятно, как до этого можно было додуматься.

fchirica

← Rev. 7 →

I tried to explain this here: http://codeforces.net/blog/entry/10476 (problem Div1. E, section "Solution fount by other contestants").

In short, let's create a function f(left, right): calculate d[j] for every j with property that left <= j <= right considering only a[i] such as left <= a[i] <= right. Answer should be fount after doing f(0, 2^22 — 1).

When you calculate f(left, right), let med = (left + right) / 2. We do divide and conquer. Let's call f(left, med) and f(med + 1, right). Now we have to "merge" the results. In [left, med], all numbers are equal to those from [med + 1, right] after switching the MSB of [med + 1, right] from 1 to 0. Hence, for i in [med + 1, right], i — (med + 1) is a submask of i (and all submasks of i — (med + 1) are submasks of i). So, we need to add d[i] += d[i — (med + 1)], for i in [med + 1, right]. After this merge step, nothing is counted twice, because when we do d[i] += d[i — (med + 1)], we add only numbers from [left, med] range. As the current range is [med + 1, right], those numbers were not added before.

Now the recursion code and yours are equivalent. That is just the iterative implementation of the divide and conquer solution explained :) BTW, this seemed magic for me, too, until I've stopped thinking it as an iterative code and I've started thinking it as divide&conquer.

SameerGulati

← Rev. 3 →

let us see where a[i] will be counted in d[]. before first iteration it is counted in d[a[i] | 0]

At each iteration of i1, i2.. affected indices are doubled. so total indices where a[i] is counted is 2^n, and all of the indices are supermasks of a[i]. Since a[i] has 2^n supermasks, a[i] is counted only once at each supermask.

cote

4 года назад, # |

I now the blog is old but I want to add a useful link here (for anyone who needs it). This is called sum over subset dynamic programming.

qingczha

This is just prefix sum on a higher-dimension array. Probably an array like a[5][5][5][5][5] might be easier to imagine how this works.

Блог пользователя popoffka