How to solve problem B ?
This problem looks similar to SPOJ-WATER
Someone please explain the approach to this problem?
Thank you!
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 164 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 159 |
| 5 | atcoder_official | 158 |
| 6 | djm03178 | 154 |
| 7 | adamant | 153 |
| 8 | awoo | 148 |
| 8 | luogu_official | 148 |
| 10 | TheScrasse | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/12/2025 15:53:39 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











I approached it in a way similar to Bellman Ford Algorithm . Take a matrix W and fill all the entries with infinity except the ones present in the border of the grid ie. i = 0 || i = (R - 1) || j = 0 || j = (C - 1) where i, j are the row index and column index respectively.
Now for each cell in the interior of the matrix water can come from 4 adjacent cells . We need to find the minimum of the incoming water from these cells and make this the new W[i][j] only if its greater than H[i][j]
For each cell with index i, j: min = min(W[x][y])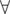 x, y adjacent to i, j and W[i][j] = max(min, H[i][j])
x, y adjacent to i, j and W[i][j] = max(min, H[i][j])
You need to run this relaxation for R * C times
My Java Code:
Link