zeref_dragoneel's blog

pairs (i,j) s.t. i^j = k
By zeref_dragoneel, history, 9 years ago, In English

number of pairs (i,j) s.t. 1<=i<=n, 1<=j<=m s.t. i^j = k in O(max(log n, log m)). I am able to do it in min(n,m).

  • Vote: I like it
  • +5
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +23 Vote: I do not like it

I will be very puzzled if that problem has a solution with logarithmic running time. And I hope that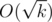 is sufficient. But if the prime factorization of k is known maybe I can solve it in .

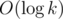Consider the prime factorization of k: k = p1k1p2k2... prkr , and we want to find a number of representations looks like ab = (p1a1p2a2... prar)b = p1k1p2k2... prkr .

Let g = gcd(k1, k2, ... , kr) . All of valid representations looks like (p1k1 / dp2k2 / d... prkr / d)d , where d is any divisor of g.

To satisfy 1 ≤ a ≤ n constraint we find min d such that (p1k1 / dp2k2 / d... prkr / d) ≤ n through binary search. It`s minimal valid d. Constraint 1 ≤ b ≤ m gives us maximal valid value of d. And answer is dmax - dmin + 1 .

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +70 Vote: I do not like it

    Hm, maybe ^ is xor?

    → Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it +9 Vote: I do not like it

    I will be very puzzled if that problem has a solution with logarithmic running time.

    But it is very easy to solve task in such representation with logarithmic running time. We just need to go through j and check

    → Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can you please share the problem link?

→ Reply
»
9 years ago, # |
  Vote: I like it +13 Vote: I do not like it

We need to find number of pairs (A, B) such that their XOR is K.
Consider binary representations of K — if some bit is 1 then respective bits in A and B must be different, and if bit is 0 then they need to be same.
Now we can represent N and M in binary and then solve it with DP[prefix][flag1][flag2].
prefix — how many bits are already placed in A and B.
flag1 — 0 if current prefix of A is same as prefix of N and 1 if it is less. flag2 is same as flag1 but for B.

→ Reply