Блог пользователя adamant

Question about suffix automaton/tree
Автор adamant, история, 8 лет назад, По-английски

Hi everyone!

As you may know, it is possible to build a suffix automaton for a set of strings as well as suffix tree consisting of all suffixes of strings from the set. Question is as follows: for each string Sk consider set Vk of vertices/states of tree/automaton that corresponds to the substrings of Sk. Is it true that 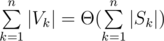? Can you prove it or make a counter-example?

  • Проголосовать: нравится
  • +46
  • Проголосовать: не нравится

»
8 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

What prevents |Vk| from being always Θ(|Sk|) for suffix trees?

→ Ответить
  • »
    »
    8 лет назад, # ^ |
    ← Rev. 3   Проголосовать: нравится +3 Проголосовать: не нравится

    We can take Sk, k > 1 as set of substrings of S1. Then |V1| will be Θ(|S1|2).

    → Ответить
    • »
      »
      »
      8 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      Set of prefixes should have the same effect. Every |Vk| is Ω(|Sk|2) then, right?

      → Ответить
      • »
        »
        »
        »
        8 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится

        Seems to be correct, cool! Then for total length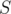 this sum will be 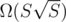and 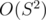. Can you improve the boundaries now?

        → Ответить