I solved this problem using Mo's algorithm.
Is there any Online solution for each query for this problem.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 151 |
| 10 | awoo | 147 |
I solved this problem using Mo's algorithm.
Is there any Online solution for each query for this problem.
| Name |
|---|



I only know the solution in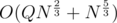 .
.
Tried to find better solution for quite a long time, but no results yet :(
Can you describe it?
Note: (I consider all values in array ≤ N. If that is not true, then you can use hashmap instead of array or with precalculations you can make that so)
precalculations you can make that so)
Split your array into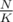 blocks with size K. Precalculate answers for all intervals between all beginnings of these blocks along with array cnt[x] which tells you how many numbers x are in that interval. You can do that simply in linear time for every interval.
blocks with size K. Precalculate answers for all intervals between all beginnings of these blocks along with array cnt[x] which tells you how many numbers x are in that interval. You can do that simply in linear time for every interval.
We have wasted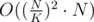 time and memory by this point, what can we do now?
time and memory by this point, what can we do now?
Let's consider we have query [L;R] such that R - L ≥ 2·K (Otherwise we can do linear search to calculate number of occurrences for every value on interval.) Now we know for sure that one of precalculated arrays is completely inside of our query. To be exact, this array covers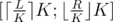 . (Further I'll call these borders [A;B])
. (Further I'll call these borders [A;B])
Notice that A - L ≤ K, same is for R - B ≤ K We can simply use the precalculated array for [A;B], recalculate the value for [L;R] with linear approach which will work in O(K) for each query.
Note: you can not copy this array, because this can take up to O(N) time, you need to use it's values without copying it and backtrack it after you're done.
You can solve this task using this idea even when you have update query (saying set Arr[i] = X), you can try it out for yourself, this isn't that hard.
To sum up: This approach works in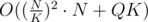 by choosing
by choosing  you can get the time complexity I was talking about.
you can get the time complexity I was talking about.
You can improve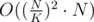 if you are using some sort of persistent structure instead of linear memory for every interval, but then:
if you are using some sort of persistent structure instead of linear memory for every interval, but then:
Most likely you will get additional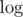 to the query procession and precalc also.
to the query procession and precalc also.
This is kinda hard for some cases
Same approach with a different k can be used
Lets say k=N^z and Q= N^y (y<=1) Total Complexity=O( N^(z*z — 2*z +2) + N^(z+y) ) We would want the two powers to be the same Equating we get: z*z — 3*z + (2-y) = 0
we get z= ( 3 — sqrt(4*y+1) ) / 2
for y=1(Q=N) , z=0.38 Total complexity = O(N^1.38)
is there any offline without mo's?
The recent solution for the problem https://codeforces.net/contest/1514/problem/D proposed by galen_colin in his recent stream on youtube, worth watching it.
Thought the problem is interesting so here is what I came up with — should be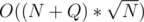 .
.
We have an array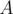 of size
of size 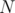 , and
, and 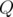 queries.
queries.
Let's start off by choosing some constant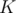 . We will do some heavy precomputing that we'll split in two parts:
. We will do some heavy precomputing that we'll split in two parts:
First precomputation
Define the following function:
We want to compute this function for all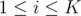 and
and 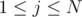 . This can be done in
. This can be done in 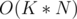 since we can do something similar to a two-pointer walk for a fixed
since we can do something similar to a two-pointer walk for a fixed  . I'll omit details, but feel free to ask.
. I'll omit details, but feel free to ask.
Second precomputation
The first part of our precomputation will help us answer queries whose answer is quite small. So we'll now have to do something about queries with a large answer. Suppose that we create a set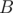 that contains all values of
that contains all values of 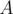 which occur in
which occur in 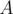 more than
more than 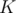 times, and denote its elements by
times, and denote its elements by 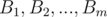 . Obviously, this set will have size of at most
. Obviously, this set will have size of at most 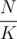 , that is
, that is 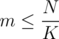 . Now let's define the function:
. Now let's define the function:
We want to compute this function for all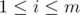 and
and 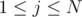 . This can again be done in
. This can again be done in 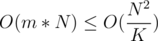 by using a DP-like approach and moving from the end to front of the array for every fixed
by using a DP-like approach and moving from the end to front of the array for every fixed  .
.
Answering the queries
Now let's start answering queries. Suppose we get a query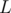 to
to 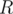 . Suppose that we want to check if there is some value that occurs at least
. Suppose that we want to check if there is some value that occurs at least 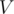 times. Well, for
times. Well, for 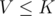 we can simply check whether
we can simply check whether 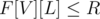 . If it is — then there is a value that occurs at least
. If it is — then there is a value that occurs at least 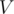 times, and otherwise there isn't one.
times, and otherwise there isn't one.
In such case, we can straight away check whether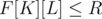 and if that's false, then we know that the answer is less than K and we can just iterate on all
and if that's false, then we know that the answer is less than K and we can just iterate on all 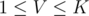 and find the largest value that works. That would take
and find the largest value that works. That would take 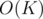 .
.
However, if we have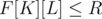 , then the answer is at least
, then the answer is at least 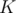 , but may be larger. Well, in that case we will check each of the numbers in
, but may be larger. Well, in that case we will check each of the numbers in 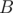 , as if the answer is larger than
, as if the answer is larger than 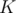 , then surely one of them is the most frequent number.
, then surely one of them is the most frequent number.
Using the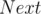 function we can easily find the number of occurrences of
function we can easily find the number of occurrences of 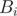 in our segment for some
in our segment for some  in
in 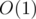 1. In such case we can find our answer in
1. In such case we can find our answer in 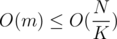 by checking every element of
by checking every element of  .
.
Resulting solution and theoretical complexity
We have total precompute complexity of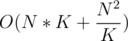 and each query is answered in either
and each query is answered in either 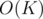 or
or 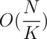 . The total complexity in the worst case is
. The total complexity in the worst case is 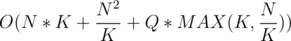 . It is plain simple to see that if we set K =
. It is plain simple to see that if we set K = 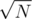 we get worst case complexity of
we get worst case complexity of 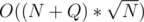 .
.
My experience
My coding and explaining are a bit rusty so writing the code and this comment took me an hour each. I ended up getting AC on the problem but with a lot of time limits prior to that. I had to optimise the code a bit to get it accepted. An example optimisation is to solve the first case of queries in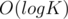 by binary search instead of linear search. I also had to pick the constant K from the program depending on the test case in order to make it run quicker, as in practice
by binary search instead of linear search. I also had to pick the constant K from the program depending on the test case in order to make it run quicker, as in practice 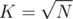 may not always be the best.
may not always be the best.
Obviously, even if the solution is asymptotically as good as Mo's algorithm offline solution, the constant is much higher, hence it's a few times slower and the SPOJ problem time limit is quite tight. Another downside of the solution is that it takes a lot of memory, but luckily the SPOJ problem had a very large limit.
Feel free to ask any questions and sorry if I've omitted too many details. Notify me about any mistakes too, as this comment took way too much time and I don't have time to proofread.
1 Note: To be able to quickly find the number of occurrences of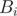 in some segment
in some segment 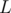 to
to 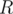 we'll have to precompute another array:
we'll have to precompute another array:
For example the sample array in the SPOJ problem {1, 2, 1, 3, 3} would yield and ID array of {2, 1, 1, 2, 1}. In a sense, we're just numbering the values of each kind backwards. Now, let's set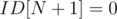 and also set all
and also set all 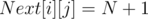 if there is no valid index
if there is no valid index 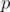 according to the definition of the
according to the definition of the 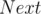 function.
function.
Now, magic! If we want to find the amount of occurrences of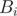 in the segment
in the segment 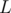 to
to 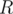 we simply take
we simply take 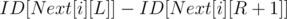 and that is our answer.
and that is our answer.
Well explained. :)
If there is update of any value, then how to solve it ?
And linear memory please.
Seriously, isn't this problem already hard enough? Encho's solution is quite complicated (and btw. I tried to solve it yesterday, spent 40-50 minutes and didn't succeed) and you just casually ask "ok, what if we also change values".
I also tried to implement that idea , but failed :(
Wow, that's really cool :) Liked magic section much
Thanks a lot , nice idea .
Great stuff! Although note that there is no need for the Next matrix, as some prefix sums would do the trick just fine! I wonder if there is some preprocessing that would let us find out information about the "frequent" elements faster than O(numberofelements). I doubt it, but it would surely be interesting to check out!
EDIT: By keeping the prefix matrix as n vectors of size sqrt(n) the solution will be very cache friendly for the big values.
There is an entry on Wikipedia: Range Mode Query.
That page mentioned an O(n) space and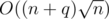 method.
method.
Theorem 1 Let A, B be any multiset.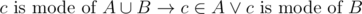 .
.
Proof Trivial
Now assume we have an array A of size n. Split it into blocks, each of which sized
blocks, each of which sized  . Precompute the mode and frequency of each consecutive blocks. It took O(n) space and
. Precompute the mode and frequency of each consecutive blocks. It took O(n) space and 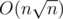 time.
time.
For each query, we have a prefix, a span and a suffix. By Theorem 1, the mode must be the mode of the span, an element of the prefix, or an element of the suffix. For each element in the prefix or the suffix, check if it is more frequent than the current mode. With additional preprocessing and analysis,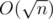 per query can be achieved.
per query can be achieved.
You can refer to the original page for more detail if you can't figure out yourself.
What if c is mode of A and B ?
Well, nothing. What do you think is the problem (issue) then?
Would you please share source? I've tried to solve it with MO O(n+q*sqrt(n)*log(n)) and got TL
Than I tried sqrt decomposition O((n+q)*sqrt(n)) with every little optimization I could and I'm still getting TL Thanks in advance.
Can't you get rid of the log n factor?
I will need some structure which supports inclusion & exclusion of elements and maximum query for O(1)... And this is impossible.
probably there is completely another way
UPD probably but it gives it in average
UPD2 Since we need just frequency and not element, it is possible to support it O(1) w.c. Thanks for forcing me to think about it again. AC with MO's
Edit: My bad, was a different problem
The LightOJ problem is different. It only deals with numbers with
consecutive frequency, so that simplifies the solution.