lmn0x4F's blog

SRM 696 Problems
By lmn0x4F, history, 8 years ago, In English

I would like to discuss last SRM problems here since I find much more comfortable CF than TopCoder forums (>.<) and it seems like they stopped publishing editorials here: Where they used to post editorials

I managed to get the first problem accepted, this was a problem with many many hacks, I think because it was kind of easy to go with a greedy approach.

My approach:

Div 1. Level 1

We're given an undirected multigraph with 50 vertices and M edges (1 ≤ M ≤ 20). We need to paint all vertices of the graph, one at a time, and after every time we paint a vertex we have to pay a fee equals the number of edges that have both ends already painted. We want to find the minimum total cost of doing so.

First we note that if we paint second vertex of edge e at time t (starting at t = 0 and increasing t after we paint a vetex) we will have to pay 50 - t in total because of this edge. So if a vertex v is the second vertex to be painted for kv edges and we paint vertex v at time tv, we will pay (50 - tv) * kv in total for this vertex. Then we see that if we're given the sequence k0, k1, ...k49 we would like to paint the vertices in increasing order of k.

To find the solution we iterate over all possible ways of orientating the M edges. For a given orientation of the graph, if edge e = (v, u) is orientated u → v means that v will be painted after u, and vice versa otherwise, also for a vertex v, kv is simply its in-degree. We calculate the cost induced by the given orientation by sorting the sequence of k's and summing up each k multiplied by 1+its index in the sorted sequence.

Is any orientation a valid one? No, it's easy to see that if an orientation has a cycle, it probably won't induce a valid order for painting the vertices, so we need to check if the orientation is acyclic. Also, the orientation could be acyclic but painting the vertices in increasing order of k won't respect the meaning of the orientation, and the cost calculated won't be the correct one, so we need to check this too, which seems more difficult. But actually we don't have to check anything :) In both cases we can prove that the cost calculated is sub-optimal, so we're happy.

Time complexity O(2M * Nlog(N)) where N = 50, the number of vertices. (We could sort in O(N) but whatever :))

  • Vote: I like it
  • +9
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Any ideas on how to solve level 2 or level 3? :D

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Ok... I found a post about this SRM... I have no idea what I looked up first time when I didn't find it...

Whatever, here it is

I can explain my solutions to div2 hard or div1 medium though, if anyone wants me to :)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yeah .. DIV 2 hard..please

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +9 Vote: I do not like it

      Here's my solution.

      Div 2. Level 3

      We're given a undirected simple graph with n vertices and we have k pair of vertices for which we don't remember whether they're connected by an edge or not. So there are 2k possible graphs. For each of them we need to calculate the size of its largest clique and return the sum of those 2k values.

      Constraints: 1 ≤ n ≤ 20, 0 ≤ k ≤ 20.

      Let K be the set of those k edges and V be the set of vertices.

      We will calculate, for all , dp[S] = size of maximum clique in the graph that has the edges in S and doesn't have the other edges in . Then the answer is just the sum over all this 2k values. We initializate this dp with 1 or 0.

      We consider each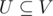 . Each U might be a clique in some of the possible graphs, we could update dp[S] for all for which U is a clique, but this would be too slow. So we'll update dp[S] only for the minimum S for which U is a clique.

      We'll use another dp for this. For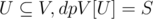 , where S is the minimum subset of K that allows U to be a clique, or invalid if such subset doesn't exists.

      Then

      • if |U| = 1.

      Otherwise we pick any vertex u in U.

      • dpV[U] =  invalid if u can't be connected to the rest of U or if = invalid.

      Otherwise let Su be the minimum subset of K that we need to connect u to the rest of U.

      .

      We calculate this dp in time O(n * 2n). After calculating it (or during) we update dp[S] = max({|U|: U such that dpV[U] = S}).

      So now dp[S] = the size of the maximum clique for which S is the minimum subset of K that allows such clique to be so.

      For each S, consider its maximum clique in the final answer, either S is the minimum subset that allows that clique, or some subset of S is that minimum subset. So for each S, the final dp we want is the maximum dp over all its subsets. We can do this in O(k * 2k) for all the sets updating the dp from small to big sets and taking maximum only over its "direct" subsets.

      time: O(n * 2n + k * 2k)

      Hope you can make sense out of it :)

      → Reply