You are given an array of numbers( N ) (a[i]<= 10^6 && N<= 10^5 ) And 10^5 Queries. In each query You will be given.
X L R.
You have to find the how many numbers are there between L to R such that ( ( a[i] & X )== X ) . Thanks in Advance
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 165 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
You are given an array of numbers( N ) (a[i]<= 10^6 && N<= 10^5 ) And 10^5 Queries. In each query You will be given.
X L R.
You have to find the how many numbers are there between L to R such that ( ( a[i] & X )== X ) . Thanks in Advance
| Name |
|---|



Auto comment: topic has been updated by khatribiru (previous revision, new revision, compare).
Suppose L = 1 and R = N for all queries. We can precalculate all answers using standart DP approach in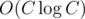 .
.
Now we want to choose some number B and divide the array to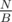 parts of size B. For all prefixes of length kB (for integer k) we will use DP approach and store all the answers. Now we can answer one query in O(B) time (sqrt-decomposition like).
parts of size B. For all prefixes of length kB (for integer k) we will use DP approach and store all the answers. Now we can answer one query in O(B) time (sqrt-decomposition like).
Total complexity: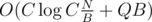 . We will choose
. We will choose 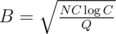 thus getting
thus getting 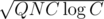 .
.
Not sure if it is good enough but better than O(QN).
Sorry, But Please explain the Dp solution for L=1 and R=N.
Suppose we have array A of length 2n. We want to calculate array B such that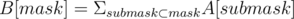 .
.
We will calculate DP[k][mask] = ΣsubmaskA[submask] where the first k bits in submask is subset of those bits in mask and other m - k are equal to bits in mask. Then DP[0][mask] = A[mask] and DP[m][mask] = B[mask].
Now how to calculate this DP:
if k-th bit in mask is 0 then DP[k][mask] = DP[k - 1][mask]
if k-th bit in mask is 1 then DP[k][mask] = DP[k - 1][mask] + DP[k - 1][mask - 2k]
It is O(n2n) or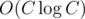 if C = 2n.
if C = 2n.
Vai, can you please share the source of the problem? The problem seems interesting :)