i_m_joey's blog

sqrt decomposition of input queries
By i_m_joey, history, 8 years ago, In English

I read about sqrt decomposition data structure on this site http://e-maxx.ru/algo/sqrt_decomposition (this site is in russian but google translate works pretty well) I have understood the standard algo of this DS in which we divide the input array into buckets of size sqrt(N) where N is the size of the array.

But here's what I cant understand:**sqrt decomposition of the input queries.**

Suppose that we have some problem in which we are given some input data, and then k queries, each of which we have to process and issue a response. We consider the case when requests are as requested (do not change the state of the system, but only asks for some information) and modifying (ie affecting the state of the system is initially set to the input data).

This is the given approach which I cant understand:split the k queries in buckets of size sqrt(k) and process all the queries in each bucket at once.

Why we decompose queries into sqrt size buckets ?? and how we can process all the queries in each bucket ??

  • Vote: I like it
  • -5
  • Vote: I do not like it

Comments Comments (8)
| Write comment?
»
8 years ago, # |
  Vote: I like it +22 Vote: I do not like it

Suppose we have two types of queries: (1) output some value, (2) change values somehow. We can build a data structure which can answer queries of type (1) fast but it is hard rebuild it after queries of type (2). Then we can do the following: we'll divide all the queries to the buckets of size B. When we have to answer to queries of type (1), we'll take the value from our data structure and then separately apply all the queries of type (2) from our bucket (they are not applied to data structure yet). For queries of type (2) we'll do nothing (at that moment). When we finish the bucket we'll rebuild our data structure applying all the queries of type (2) at once. So there will be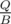 rebuildings and we answer each query of type (1) in O(f + B) time where f is the time of handling one query by the data structure we used.

Now I'll try to apply this idea to easy problem (which can be solved in many other ways).

We have an array of integers and queries of 2 types: (1) get sum on segment [l: r] (2) change value at position pos. If there will be only queries of type (1) then we'll calculate prefix sums and answer all the queries in O(1) time. But it is hard to rebuild prefix sums when we change 1 element. But we can use the above approach and rebuild it only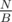 times. Answering the query of type (1): take the answer from prefix sums, then check if we change some elements inside the segment [l: r] in the last block of queries. Total complexity will be 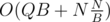. We can choose 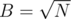and get 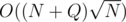. But we can choose 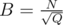and get 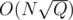. In most applications it is the same though.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    thanks a lot, really very helpful :)

    just one doubt more..In the problem of disjoint-set-union division (an example of sqrt decomposition), why we remove all the edges from the graph and then build dsu at the beginning of each query block the edges that will be deleted in this block ?

    because the requests can be in order (1)check whether (x,y) connected.(2)delete (x,y) (3)check whether (x,y) connected.....How can we delete all the edges at the beginning ?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      I'm not sure if I correctly understand the problem you've mentioned. There is a graph and queries like (1) add edge vu (2) delete edge vu (3) check if v and u is in the same connected component ?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        yup, u understand it correctly.

        There is an undirected graph with n vertices and m edges. There have been three types of requests: to add an edge (X_i, y_i), remove the edge (X_i, y_i), and check whether or not bound peaks x_i and y_i through.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          The idea is to to change operations (add edge) and (delete edge) to operation (there is an edge from time t_l to time t_r). Now we can divide into time into blocks. For each block there are only edges that can change its state during the block. So we'll add all edges which are existing through all the block and compress components. Now we have graph with only edges and we can simply run DFS to check if two vertices are connected.

          And you should to read this post.

          → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    in the last block of queries

    1. Do you mean the current block?

    2. And can you please explain how to check if we changed some elements inside some segment efficiently?

    3. Should I use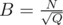 when Q > N?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      1. We are processing blocks from left to right. So the current block is the last one we have seen.

      2. We should try all the changes in the current block.

      3. Theoretically it is always better to use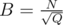 . In practise you should use that value of B which works better.

      → Reply