First, suppose n is the shortest side of the triangle, m, k are other two sides. According to Pythagorean Theorem, we know n2 + m2 = k2
just do a change k2 - m2 = n2
futherly (k + m)(k - m) = n2
as we know, n2 × 1 = n2 so we can suppose that k + m = n2, k - m = 1 [because we have SPJ]
easily, we get 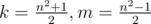
because the side is a interger, so this solution can only be used when n is a odd.
So how to deal with even? we find that if (k-m) is odd, the solution is suitable for odd. On the other hand, we guess that if(k-m) is even, the solution is suitable for even.
just as this, 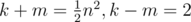
so, we get 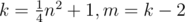
this is an O(1) algorithm.
So if you want to see more clearly, you can see the formual on this page. if you have some questions, i am willing to help you.:) [my english is not very good, so please pass some grammer fault.:P]











Auto comment: topic has been updated by PengsenMao (previous revision, new revision, compare).
why did you remove the anime background solution. This is how all solutions should be presented.
well, at first, i thought CF don't support LaTex. So i added this picuture to let others see the formula But a very kind buddy told me how to print LaTex. therefore, i thought it's no necessary to keep this picuture on this solution:P
How do you prove that n is a cathetus of any right triangle ?
We don't need to mind that because we have a special judge. suppose it is a short side is much easier to solve.
Thank you for your explanation! It's really helpful.
I have a question.
This solution indirectly imply that every hypotenuse of some valid triple is always cathetus (leg) of other valid triple (since by definition of the task they would give you cathetus (leg) as well as hypotenuse). If it were not true your formulas would not work. But your formulas work well, so it's true.
How do you prove this? (every hypotenuse of some valid triple is always cathetus (leg) of other valid triple)
We don't need to mind that because we have a special judge. suppose it is a short side is much easier to solve
What do you mean special judge? The problem states that:
As I can see why your solution works: if you given hypotenuse c such that a2 + b2 = c2 form Pythagorean triple, then there is another valid Pythagorean triple such that c2 + x2 = z2 and therefore you calculate other sides x, z from c as cathetus (leg).
The question is why if a2 + b2 = c2 is Pythagorean triple then exists another Pythagorean triple such that c2 + x2 = z2?
you know, there are multiple answers, right?So the case that n is a short side is exist.
Yes, there are multiple answers but my question is different.
Suppose you are given in some test case n as hypotenuse of some valid triple a2 + b2 = n2. If there are no other valid triple where n is cathetus (leg) such that n2 + y2 = z2 then your solution would not work because your formulas work only if n is cathetus.
But in practice, I see for every valid triple a2 + b2 = n2 there is another valid triple such that n2 + y2 = z2.
For example, let's take triple (8, 15, 17), 17 is hypotenuse here. Luckily, there another valid triple where 17 is cathetus (17, 144, 145). In practice for every valid (a, b, c) there exists (c, x, z).
But why? I don't understand. I thought about some number c which only exists as hypotenuse in some triple (a, b, c). In turns out that this number doesn't exist.
You can't just assume that you can interpret any n as cathetus. You have to prove that it's actually true.
May be you didn't take into account this fact and just luckily gets accepted.
I want mathematical proof of this fact.
there must be such case, because any n(n>2) can find m, k that n^2 + m^2 = k^2
Amazing! I didn't know that. Thanks!
I thought there are "holes" where for some n you can't find m, k such that n2 + m2 = k2.
It turns out your formulas can be used to prove by induction (base case 3) that for any n there is m, k such that n2 + m2 = k2.
UPD: I was confused by this article: formulas for generating Pythagorean triples. I thought that if you need such complicated methods for generating Pythagorean triples, there should be numbers for which Pythagorean triples doesn't exist.
UPD2: I see what this wiki article is talking about. The article discuss methods to generate all possible valid triples. For example, all of these triples are valid (9, 12, 15), (9, 40, 41), (12, 35, 37) but your method generate only (9, 40, 41) and (12, 35, 37) but not (9, 12, 15). While methods discussed in this article allow to generate triples such as (9, 12, 15). I.e. your method is enough exactly what task 707C require ( find any valid triple for n ).
Actually all those mathematical formulas from the top of the post ARE proof that any n>2 can be used as a cathetus in a pythagorean triangle. That's the whole point of the post.
The formulas prove every n is cathetus of a valid triple, so the valid hypotenuses definitely are too, right?
it doesn't matter whether n is cathetus of a valid triple. n can be short side or hypotenuse, but suppose it is a short side is eaiser for us to solve.
I clarify my question. Please, see my comment above.
You missed my point. His formulas show that you can find a triangle with n as cathetus for any integer n ≥ 3.
So clearly there isn't an integer a2 + b2 = n2 that isn't a cathetus simply because there isn't any integer at all that isn't a cathetus.
but we choose n as the shortest side is not wrong.
Thanks! Now, I understand.
"because the side is a interger, so this solution can only be used when n is a odd." but why? i dont understand it.can u explain pls?
when n is an odd, (n^2+1)%2=0, so that the side is an interger. just reverse that.
PengsenMao thank you very much but i had another view
for any triangle pythegorean
a =m^2 — n^2 b = 2 *m *n c= m^2 + n^2
where m>n and one of them is odd and one of them is even and gcd(n,m)=1
so a is always odd and b is always even . given x . if x is even then x =b x =2 *m *n now i should assume m and n to satisfy the condition n=1 odd m =x/2 even because x>=4 even number and gcd(1,m)=1 true for condition. so we get a and b .. and if x is odd it will be equal a.. is my approach right for now ?
I am not quite sure coz i don't get u clearly :(
would u like to be more specific?
"because we have SPJ" wat ?
He only meant Special judge. To be more specific, the judge is accepting any valid triplet. Like suppose you are given a number x as an input so (a,b,x) and (x,y,z) both are acceptable. But the point of the whole proof is to prove that for any valid triplet (a,b,c) where c is acting as an hypotenuse there exists at least one triplet where this c acts as a leg(smallest) side which is of the form of (c,d,e).
Great solution, thanks for editorial it was not available on editorial page.
thanks for writing this one.