Sorry but I do not know if this has a solution:
Given the area of ABKI, CDLJ, ACOM, BDPN and ABDC. Can we find area EFGH?
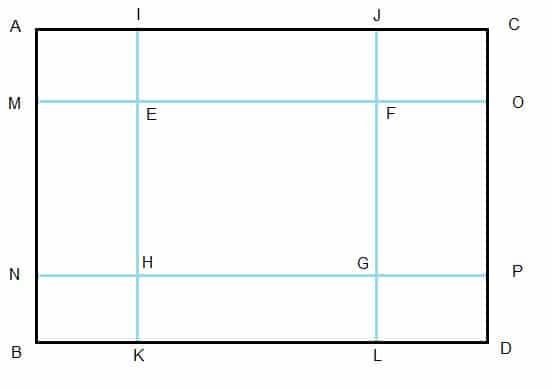
Thanks!
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 151 |
| 10 | awoo | 147 |
Sorry but I do not know if this has a solution:
Given the area of ABKI, CDLJ, ACOM, BDPN and ABDC. Can we find area EFGH?

Thanks!
| Name |
|---|



Yes, we can. Moreover, areas of all rectangles can be determined. Although we have 6 degrees of freedom for the sides of the rectangles, there are only 5 degrees of freedom for their areas. You can expand the picture horizontally by X times and contract vertically by X times and all areas will remain the same.
Sorry, didn't get it. what's "5 degree freedom of area"? And how to expand and contract area? Please elaborate!
Thanks! :)
You're welcome! :)