Problem Statement: https://www.codechef.com/COOK73/problems/MADHAT
My implementation: http://ideone.com/u9Av7q
Here's what I did:
First, I assigned temp[i] to the index of kid with just higher IQ than IQ of kid at index i (as per the given data). filltemp is the recursive function to assign temp[i] to each i. (temp[i] for kid with maximum IQ is n) (Check example below for details)
Then, the answer should be the number of topological orderings in tree with directed edges from temp[i] to i, starting from kid with with maximum IQ.
To find the number of topological orderings, I used dfs as each branch of tree is independent.
I'm getting WA for this implementation, can anyone explain the test case that'll give WA on this?
Example:
n=4 x=[0,2,1,0]
I know following relations using x.
- IQ[1]>IQ[0] since x[0]=0
- IQ[2]<IQ[1] and IQ[3]<IQ[1] since x[1]=2
- IQ[3]<IQ[2] since x[2]=1
So my temp becomes [1,4,1,2] and the edges in tree are 4->1, 1->0, 1->2, 2->3
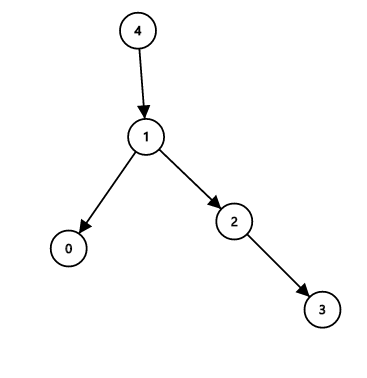
The number of topological sorts are 3, which is the right answer for this test case.
Why number of topological orderings is the answer? Because, suppose I traverse the tree in this order: 1,2,0,3. Now I'll assign IQ of kids in decreasing order from n to 1 as per the sorting. That is, IQ[1]=4, IQ[2]=3, IQ[0]=2, IQ[3]=1.
Other topological orderings for this example are 1,2,3,0 and 1,0,2,3 which generates two other respective IQ array.











your code fails on
1
3
2 1 0
Thanks for the test case. It was a minor implementation mistake on my part. I've updated the code, but its still giving WA. Any further hints?
BLOG IS COOL!
LOL
KEK
GGWP EASY
NICE