Пожалуйста, задавайте возникающие у вас вопросы по задачам. Особенно это касается задачи D, так как она оказалась наиболее сложной.
Задача <<Экзамены>> По условию 2n ≤ k ≤ 5n. Если k < 3n то некоторые экзамены мы сможем сдать только на 2. Таких будет 3n - k. Если же 3n ≤ k, то мы все экзамены сдадим как минимум на три.
Задача <<Квадрат>> Пусть карандаш идет по прямой и ставит крестики через каждые (n + 1) точку. Поставим в соответствие положению на прямой положение на квадрате. А именно, точке x на прямой будет соответствовать точка, в которую придет карандаш, сдвинувшись по периметру квадрата на x. Тогда левому нижнему углу квадрата соответствуют все точки вида 4np для некоторого целого неотрицательного p. Поставленным крестиками будут соответствовать точки k(n + 1). Самая ближайшая точка совпадения двух семейств, за исключением начальной, будет в LCM(n + 1, 4n) (LCM — НОК). Тогда всего мы поставим 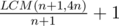 крестиков.
крестиков.
Задача <<Разрезание фигуры>>
Основная идея: учитывая, что ответ не превышает двух, проверим существование ответа 1.
Докажем, что ответ в задаче не превосходит двух. Пусть площадь фигуры не менее 4. Тогда рассмотрим самую левую из самых верхних клеток. У нее нет левого и верхнего соседей по стороне. Значит, у нее не будет более двух соседей. Тогда, удалив ее соседей мы уже разделим фигуру на две. Если площадь равна трем, то всегда можно разрезать ее, удалив одну клетку, это можно проверить, так как существует всего два принципиальных случая. Если площадь фигуры не превышает двух, то какое бы множество клеток мы не удалили, она не распадется.
Проверим, существует ли ответ, величины один. Удаляемую клетку можно просто перебрать, а затем запустить dfs из любой неудаленной клетки. Если dfs посетит не все оставшиеся клетки, то, удалив нужную клетку мы разрежем фигуру. Если подходящая клетка нашлась — ответ равен 1. Если нет — 2.
Еще нужно было не забыть, что иногда ответа может просто не существовать. Это бывает тогда, когда площадь фигуры меньше либо равна двум (площадь фигуры — кол-во клеток в ней)ю
Асимптотика решения O(n4). Еще можно было воспользоваться алгоритмом поиска точек сочленения и решить эту задачу за O(n2). Но это, наверное, требовало больших трудозатрат.
Задача <>
Основная идея: перебор за O(Fun). Fu — u-е число Фибоначчи.
У этой задачи было довольно сложное условие. С массивом a можно было проводить операции двух типов. Нужно было провести ровно u таких операций, чтобы максимизировать сумму значений массива с заданными коэффициентами.
Если просто перебрать все возможные комбинации операций, а потом промоделировать их, то получится решение за O(2u·nu). Это слишом долго. Можно было улучшить это решение, перебирая комбинации операций рекурсивно и по ходу рекурсии моделируя их. Тогда асимптотика улучшается до O(2u·n). Собственно, ничего сильно лучше этого решения не требовалось. Возникает лишь одно соображение: если у нас были две операции  подряд, то они ничего не изменили и их можно переместить в любое место нашего алгоритма, не изменив его результат. Тогда можно перебирать только те алгоритмы, в которых все парные операции
подряд, то они ничего не изменили и их можно переместить в любое место нашего алгоритма, не изменив его результат. Тогда можно перебирать только те алгоритмы, в которых все парные операции  стоят в конце. Это тоже можно было делать рекурсивно, не идя в ветки с двумя, подряд идущими операциями
стоят в конце. Это тоже можно было делать рекурсивно, не идя в ветки с двумя, подряд идущими операциями  и обновляя лучший ответ не только в конце рекурсии, но и тогда, когда в конце осталось четное число операций. Это работает сильно лучше. Вспомнив известную задачу "кол-во последовательностей из нулей и единиц, без двух единиц подряд" можно понять, что кол-во таких последовательностей, длиной k, равно Fk + 1, где Fi — i-е число Фибоначчи. Тогда кол-во допустимых алгоритмов равно сумме первых u чисел Фибоначчи. Эта сумма примерно равна (u + 2)-му чмслу Фибоначчи. Итоговая асимптотика составляет O(Fu·n). Для максимальных значений входных данных эта величина равна примерно 30 миллионам.
и обновляя лучший ответ не только в конце рекурсии, но и тогда, когда в конце осталось четное число операций. Это работает сильно лучше. Вспомнив известную задачу "кол-во последовательностей из нулей и единиц, без двух единиц подряд" можно понять, что кол-во таких последовательностей, длиной k, равно Fk + 1, где Fi — i-е число Фибоначчи. Тогда кол-во допустимых алгоритмов равно сумме первых u чисел Фибоначчи. Эта сумма примерно равна (u + 2)-му чмслу Фибоначчи. Итоговая асимптотика составляет O(Fu·n). Для максимальных значений входных данных эта величина равна примерно 30 миллионам.
Мне не удалось написать на эту задачу отжиг или какое-либо рандом-решение, которое проходило бы все или хотя бы большинство тестов.
Задача <<Расстояние Хемминга>>
Основная идея: сведение к СЛАУ и решение ее методом Гаусса.
Заметим, что если мы одинаковым образом переставим символы во всех строках, то ответ не изменится. Рассмотрим <<столбцы>> ответа, то есть строки s1, i + s2, i + s3, i + s4, i для некоторого i. Всего существует 24 = 16 типов таких строк. Получается, что, если существует ответ на задачу, длины l, то существует и ответ той же длины в котором столбцы упорядочены по типу. Тогда, чтобы перебрать ответ, достаточно перебрать 16 чисел — количества столбцов каждого типа. По этим числам легко восстановить все расстояния Хемминга. Расстояние между строками si и sj будет равно сумме количеств столбцов в которых различны символы c номерами i и j.
Однако перебирать все возможные количества столбцов каждого типа слишком долго. Заметим, что мы можем записать систему из 6 уравнений с 16 неизвестными (вспомнив, что расстояние между строками si и sj будет равно сумме количеств столбцов в которых различны символы c номерами i и j). Неизвестными в этой системе уравнений будут количества столбцов каждого из типов. Заметим, что некоторые варианты столбцов полностью идентичны с точки зрения вклада, вносимого в расстояния Хемминга. А именно, столбцы, получаемые друг из друга инвертированием всех букв (заменой <> на <> и наоборот) вносят идентичный вклад в расстояния Хемминга. Например, если добавить в ответ столбец <>, расстояния Хемминга между всеми парами строк изменятся тем же образом, что и при добавлении столбца <>. Получается, что мы можем рассматривать лишь 8 возможных столбцов. Кроме того, столбцы <> и <> вносят нулевой вклад во все расстояния Хемминга. Один из них мы уже исключили из рассмотрения, но можно исключить и второй. Таким образом, мы сократили количество переменных до 7. Решим СЛАУ относительно каких-нибудь шести переменных. Свободным осталось значение одной из переменных. Так как столбцы, количеству которых соответствует эта переменная, вносят ненулевой вклад хотя бы в одно расстояние Хемминга, значение этой переменной не может превосходить максимума из заданных расстояний Хемминга. Тогда можно перебрать его и выбрать наилучший из получившихся ответов.
Алгоритм получается следующий:
- Для каждого типа столбцов определим, какой вклад один такой столбец вносит в каждое из расстояний Хемминга
- Запустим алгоритм Гаусса для полученной матрицы
- Переберем значение свободной переменной, выразим через нее остальные, проверим, что все они неотрицательны и целы, выберем наилучший из ответов.
- Выведем ответ.
Асимптотика этого решения составляла O(max(di, j)), если пользоваться типом double и 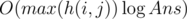 , если решать задачу в рациональных числах.
, если решать задачу в рациональных числах.
Наверное, могло показаться, что при решении в рациональных числах могло быть переполнение. Но, так как мы применяем наш алгоритм к одной и той же матрице (за исключением последнего столбца), наши вычисления всегда одинаковы, то есть мы домножаем строки на одни и те же числа. Можно заметить, что в нашей матрице все числа будут единицами или двойками, тогда никакой коэффициент в итоге не превысит 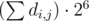 . Таким образом, можно решать задачу в рациональных числах или в типе double.
. Таким образом, можно решать задачу в рациональных числах или в типе double.
Задача <<Два отрезка>>
Основная идея: обратить перестановку и решать упрощенную задачу (см. ниже), рассмотреть функцию <<количество отрезков в перестановке, которые образуют данный отрезок натурального ряда>>.
Чтобы решить эту задачу, можно решить обратную: <<дана перестановка pn, нужно посчитать в них количество отрезков, элементы которых образуют 1 или 2 отрезка натурального ряда>>.
Если мы решим эту задачу для некоторой перестановки qn, такой, что 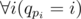 , то мы получим ответ для исходной задачи и перестановки.
, то мы получим ответ для исходной задачи и перестановки.
Первое решение, которое приходит в голову: переберем отрезок перестановки и в булевом массиве отметим элементы, принадлежащие ему. Проверим, что в булевском массиве получилось два отрезка. Такое решение будет иметь асимптотику O(n3).
После некоторых размышлений можно понять, что при переходе от отрезка пере [l, r] к [l, r + 1] количество отрезков изменится некоторым предсказуемым образом. Обозначим s([a, b]) количество отрезков, которые образуют элементы отрезка [a, b] перестановки. Если новый элемент pr + 1 будет находиться между уже поставленными элементами (то есть, элементы со значениями pr + 1 - 1 и pr + 1 + 1 будут принадлежать отрезку [l, r]), то s([l, r + 1]) = s([l, r]) - 1. Новый элемент <<склеит>> два отрезка между которыми появится. Если у элемента pr + 1 будет один сосед, принадлежащий отрезку [l, r], то s([l, r]) = s([l, r + 1]) (один из существующих отрезков удлинится). Если же у элемента pr + 1 не будет соседей на отрезке [l, r], то новый элемент образует новый отрезок и s([l, r + 1]) = s([l, r]) + 1. Это иллюстрирует рисунок ниже:

Новый элемент помечен красным, уже поставленные — черным.
Из этих соображений можно получить следующее решение: переберем левую границу и, перебирая правую слева направо, будем пересчитывать количество отрезков, которые образует текущий отрезок перестановки. Если это число равно 1 или 2, прибавим к ответу единицу. Получаем асимптотику O(n2). Это решение работало достаточно быстро даже на n = 20000. Но, разумеется, этого было недостаточно, чтобы решить задачу.
Перейдем к полному решению. Оно основывается на предыдущем. Мы уже умеем пересчитывать число отрезков при движении правой границы. Теперь нужно понять, как найти s([l - 1, r]) для любых r, используя s([l, r]). Будем перебирать позицию левой границы отрезков справа налево и поддерживать структуру данных, которая позволит нам хранить s([l, r]) для всех r и сможет считать в себе количество чисел 1 и 2.
Обозначим за Δi s([l - 1, i]) - s([l, i]). Δl = 1 так как один элемент образует ровно 1 отрезок. Далее, если мы будем увеличивать i, Δi будет зависеть от количества соседей элемента l на отрезке [l - 1, i].
- Если на отрезке нет соседей l, то количество отрезков, которым он соответствует увеличится на 1 при добавлении элемента l (так как l не присоединится ни к какому существующему отрезку).
- Если на отрезке ровно один сосед l, то количество отрезков, которым он соответствует не изменится при его добавлении (так как l просто присоединится к отрезку своего соседа).
- Если на отрезке два соседа l, то при его добавлении, количество образуемых отрезков уменьшится на 1.
Найдем соседей l, лежащих после него. Обозначим их за a и b. (если после l лежит только один его сосед, b = inf) тогда для всех i, таких что l ≤ i < a Δi = 1. Для всех i, таких что a ≤ i < b Δi = 0 и для всех i удовлетворяющих b ≤ i ≤ n Δi = - 1. Тогда, чтобы обновить нашу структуру достаточно сделать два прибавления на отрезке.
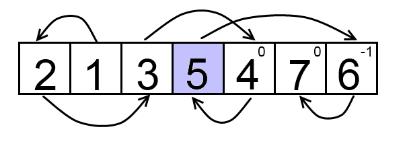
На картинке выше видно, что у элемента 5 оба соседа лежат правее его. Поэтому получается три отрезка эквивалентности Δi (первый из них находится в самом элементе 5). После первого встреченного соседа (4) Δi принимает значение 0 и, наконец, начиная с соседа 6, Δi принимают значение - 1.
Остается только придумать структуру, позволяющую прибавлять на отрезке +1 и -1 и искать в семе числа 1 и 2. Во-первых, заметим, что неположительных чисел структура хранить не будет. Тогда числа 1 и 2 будут являться первым или вторым минимумом в структуре. Тогда структуре достаточно уметь искать два минимума в себе и уметь прибавлять +1 и -1 на отрезке. Два минимума ищутся почти так же, как и один, поэтому можно адаптировать дерево отрезков или sqrt-декомпозицию под эти цели. Сумма ответов структуры на каждой итерации будет ответом на задачу. Авторская sqrt-декомпозиция работала 1.3 секунды, авторское дерево отрезков — 1.1 секунды. sqrt-декомпозиция на Java — 3.6 секунд.
Задача <<Число Фибоначчи>>
Решение: baby-step-giant-step
В этой задаче было дано некоторое число Фибоначчи f по модулю 1013, требовалось определить его первое вхождение в последовательность (позицию).
- Рассмотрим два взаимно простых модуля, делящих 1013. Пометим их как a и b.
- Остаток от деления f на a будет равен остатку от деления настоящего числа Фибоначчи F, такого, что
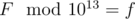 . (
. (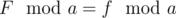 ).
). - Найдем вхождения
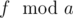 в период последовательности Фибоначчи по модулю a.
в период последовательности Фибоначчи по модулю a. - Найдем вхождения
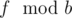 в период последовательности Фибоначчи по модулю b.
в период последовательности Фибоначчи по модулю b. - Зафиксируем пару этих вхождений. Пусть вхождение в последовательность Фибоначчи по модулю a будет в позиции i, а по модулю b — в позиции j.
- Обозначим за t(m) период последовательности Фибоначчи по модулю m.
- Из Китайской Теоремы об Остатках следует, что t(ab) = LCM(t(a), t(b)) (так как a и b выбраны взаимно простыми).
- Тогда по зафиксированным вхождениям f по модулям a и b можно восстановить вхождение f в последовательность по модулю ab. Это можно сделать, решив Диофантово уравнение i + t(a)·x = j + t(b)·y. Это уравнение можно решить перебором одного из корней.
- Если найденное вхождение в последовательность по модулю ab обозначить за u, то все вхождения f в последовательность по модулю 1013 будут представимы в виде t(ab)·k + u. Тогда переберем k и найдем все вхождения f в последовательность Фибоначчи по модулю 1013. Чтобы получить из числа Фибоначчи на позиции α, чиcло Фибоначчи на позиции α + t(ab) нужно домножить вектор из Fα и Fα + 1 на некоторую матрицу.
- Выберем a = 59 и b = 213. Заметим, что никакое число не входит в период последовательности Фибоначчи по каждому из этих модулей более 8 раз. Тогда пар вхождений будет не более 64. Для каждого вхождения мы переберем до
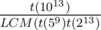 чисел.
чисел.
Еще можно было более эффективно воспользоваться тем, что число вхождений любого числа в период последовательности Фибоначчи по модулям вроде 10k невелико. Можно было получать из вхождений числа f в последовательность по модулю 10i получить вхождения по модулю 10(i + 1) подобно тому, как в авторском решении осуществляется переход от модуля ab к модулю 1013.











B(div 2) можно было написать и без LCM. LCM(4 * n; n + 1) > 0, если (n + 1) либо кратно 4, либо 2. Поэтому код сводится к следующему:
Да, это одно из авторских решений. Можно было это понять рассуждая как-то так: когда мы попадем в какой-нибудь угол, задача сведется к симметричной. Если попадаем в соседний, то в свой попадем за в 4 раза больше ходов. Если в противоположный — за в 2 раза больше. Если в свой — понятно. В угол мы всегда попадем за n шагов. В какой угол мы попадем первым можно понять по остатку от деления на 4.
Дайджест комментариев соседнего поста:
Более простое решение С див 1: http://codeforces.net/blog/entry/4671#comment-95216
Решение СЛУ без дробных чисел: http://codeforces.net/blog/entry/4671#comment-95211
В E придумал решение, использующее идею meet-in-the-middle. Её можно решить быстре чем за ?
?
Да. Постепенно домножаем модуль на 2/5, поднимая ответ.
Точняк. Мы же умеем понимать, как меняется решение сравнения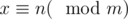 с переходом от m к 5m. Круто!
с переходом от m к 5m. Круто!
Авторское решение было за O(59 + 213 + 54 * 64 * 64 * ...). Мы брали два модуля 59 и 213, искали вхождения f по соответствующему модулю в эти две последовательности, далее объединяли их, получали вхождения по модулю 59·213 и далее по каждому вхождению пробегали по всем числам, которые имели нужный остаток по модулю 59·213 (домножая на матрицу). Это довольно быстро работало, но участники придумали решение и попроще, и побыстрее, и куда красивее.
Сначала идея была в том, чтобы получить из вхождений по модулю 10k вхождения по модулю 10(k + 1). Это делалось просто пробегом по вхождениям по модулю 10k и для каждого из них генерацией возможных вхождений по большему модулю.
Все эти решения основаны на том, что вхождений любого числа Фибоначчи в один период последовательности по используемым модулям весьма мало. Для авторского решения это можно просто проверить, поскольку этот факт используется только для двух константных модулей. Не знаю, как доказывается работоспособность решений участников.
Да, у меня один-в-один ваше, только я получил вхождения для 510·213.
Немного более простое (имхо) объяснение по D:
Нам нужно, чтобы числа с L по R образовали не более двух отрезков в нашей перестановке.
Давайте чтобы посчитать отрезки, посчитаем их первые элементы: чисел таких, что оно само от L до R, а предыдущее число в перестановке не от L до R. Их будет ровно столько же, сколько отрезков.
Теперь вопрос — а для каких L и R заданное число будет первым элементом отрезка? Пусть наше число A, а предыдущее число в перестановке B. Тогда если B<A, то для всех отрезков с B+1<=L<=A, A<=R, а если B>A, то для всех отрезков с L<=A, A<=R<=B-1.
Теперь у нас есть набор прямоугольников на плоскости, и нужно узнать сколько точек они покрывают не более 2 раз. Дальше как написано в разборе — дерево отрезков.
Да, кажется, понял. Вы с другой стороны совсем подошли. Но фактически то же. Я так и не придумал, как эту идею коротко и понятно изложить =(
Обозначим за Δi s([l + 1, i]) - s([l, r]). Δl = 1 так как один элемент образует ровно 1 отрезок. Далее, если мы будем увеличивать i, Δi будет зависеть от количества соседей элемента l на отрезке [l + 1, i].
Наверное, "Δi s[l -**(минус)** 1,i] — s([l, i**(не r)**])"? Из-за этой строки некоторое время не мог въехать. И дальше тоже l — 1, ведь мы сдвигаем левую границу всех промежутков влево..
Ох, да, спасибо. Извините.
Кто-нибудь может рассказать, как нормально загружать с дропбокса картинки? Вернее, вставлять в текст.
I did it in O(n^2). I always do. It was a really nice problem, everyone got hacked :)
В "разрезании фигуры" стоит добавить пояснение для тупых, когда нет решения. В "Xor" только к концу становится ясно, что Fu — u-тое число Фибоначчи. Хорошо бы пояснить сразу. Вот =)
По-моему, в задаче "Разрезание фигуры" асимптотика не О(n^4), a O(n^2*m^2), там ведь клеток n*m. Или я чего-то не понимаю?
Всё верно понимаете. Для упрощения (так как максимальные значения n и m совпадают) в асимптотике указывают только одно, получается четвёртая степень.
наверное ещё одно решение по С: жадность. Поки есть по крайней мере одно d[i][j]>0 делать: Ищем маску 0..7, в которой суммарное к-тво отличающихся битов максимальное и которое не приводит нас в ситуацию где ответ -1, а именно : для всех i,j,k должно быть: d[i][j]>=0 && d[i][j]+d[j][k]>d[i][k]. Если такой нет то ответ -1. Дописываем соответствующие цифры к ответам. В конце получаем ответ.
Как доказать что ответ оптимальный по длине не знаю. Но тесты проходит.
Is problem ““Hamming distance” perfectly designed?
I mean if the strings number is not 4,such as 5,6,7 or bigger,than the number of variables will much bigger than equations number,How can we solve it in this situation?
Is Problem “Hamming distance” perfectly designed?
I mean if the number of strings is not 4,such as 5,6,7 or bigger,the number of variables is much bigger than equation number.How can we solve it in this situation?
It's solvable, yes. We have system of linear equations and limitations (all values must be non-negative). In that case you can use simplex-mathod and Homori method. I can't tell you more because i'm not sure how it works. But it's so hard for me, and it's not beautiful in my opinion.
I think this solution still works but you have to set a new equation system, and it's going to be more than 7 variables. The rest of the algorithm should be the same.
But in this solution,we need to enumerate more than one free variables.
That was exactly my solution for xor but I got TLE...
Maybe, you didn't really cut off the branches which have two xors in a row in the recursive tree.
Your solution have right complexity, yes. But it's so slow because of using vector as parameter in recoursive function. Test 3 is not maximal test. Optimise your solution, remove vectors, long longs etc. And it will pass the tests.
ah thanks
I don't quite get this. How do you get rid of the u factor?
Edit : Ah nvm. I see it now :).
"Асимптотика решения O(n4). Еще можно было воспользоваться алгоритмом поиска точек сочленения и решить эту задачу за O(n2). Но это, наверное, требовало больших трудозатрат."
Вот похоже http://codeforces.net/contest/194/submission/1757313 что за квадрат, без точек сочленения (а может это и есть алгоритм поиска точек?).
Может кто нибудь объяснить как это работает?
Обычный поиск точек сочленения. Соответствие названий переменных с кодом из http://e-maxx.ru/algo/cutpoints : vis — used, tm — timer, d — tin, lw — fup, a — количество точек сочленения. Ну и тут не строят граф явно, а ходят по матрице.
One variable steel be free. Let’s fix it. It’s value can’t be more than maximum of h(si, sj) because column adds positive value to one or more Hamming distance. For every fixed value we should check if all variables take non-negative integer value and choose the best answer.
what do you mean ???? which variable????
We have six linear equations with seven variables. Number of variables greater than number of equations. Because of this we have one free variable. In other words we can represent every variable except for free as f(x) where x is free variable.
For example there are one free variable in this system of linear equations:
x, y and z can be free because we can represent any two variables as f(a) where a is free variable. Is it clear?
Sorry for my English..
I mean how did you get the last restriction ?
The number of columns is fixed ?
Why it can’t be more than maximum of h(si, sj)?
I think your prove might be insufficient,because the column's contributions to hamming distances are not arbitrary,it have some pattern.
Look, every column except <> and <> (we don't use it) add 1 to some h(si, sj) because there are two different letters in every such column. For example, if we add column <> to the answer h(s0, s3) will increase by one (h(s1, s3) and h(s2, s3) will increase too). Therefore number of every type of columns doesn't exceed h(si, sj) if letter i differs with letter j in this column. We obtain that number of every type of columns doesn't exceed some h(si, sj). Then number of every column doesn't exceed maximum of h(si, sj).
about div1 Problem E, how to count t(10^13)?
In ques A of Div 1, let us say the grid/matrix : )
)
How can deleting 2 cells eventually disconnect the whole component? If corner of the grid is deleted, then also some column will certainly have a colored cell sharing a side, just beneath it. Am I doing it right?
We denote the row number from up to down as 1,2,..., and the column number from left to right as 1,2,.... If we delete (row=1,column=2)-th and (row=2,column=1)-th cells, the original graph will be disconnected, since the (row=1,column=1)-th cell has been isolated from the other part.
As a feasible solution, we could check the degree of each cell, and if some cell has degree-1, then the answer is 1 by deleting its unique neighbor; otherwise, we could find a cell with degree-2, and deleting its two neighbors gives answer 2. If can be proved that there exists at least one cell with degree-2.
Got it.Thanks!
it will fail on TC-7
You are right, and thank you for pointing out my mistake. Test 7 is a nice counter-example to my solution described above. I think the correct one is to run tarjan algorithm to find if there exists a cutting node. If yes, the answer is 1, and ohterwise it should be 2.
yes