RazvanD's blog

Hackerrank — Beautiful 3 Set
By RazvanD, history, 8 years ago, In English

https://www.hackerrank.com/contests/world-codesprint-6/challenges/beautiful-3-set

I can't quite understand how to solve the problem. Although there is an editorial it's really poorly written as it only explains how to get an upperbound for the number of sets but it doesn't explain why that upperbound is achievable and how to come up with a formula for the numbers that satisfy the bound.

Thanks in advance.

  • Vote: I like it
  • +28
  • Vote: I do not like it

Comments Comments (5)
| Write comment?
»
8 years ago, # |
  Vote: I like it +14 Vote: I do not like it

I too cant understand the editorial.During the contest I wasted a lot of time on this problem trying to model it into some sort of matching problem.Does a matching solution exist for this problem?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    IMHO,no. General case for this problem is Rainbow Matching which is NP-hard. But, I've read somewhere in the web that for perfect bipartite graphs lower bound (2 * n) / 3 exists.

    → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it +17 Vote: I do not like it

why that upperbound is achievable

The simplest and the best proof of this is to show by example.

how to come up with a formula

Actually, there are a lot of formulas. I can show how i came up with my solution.

At first, I decided to take first set as 0 1 2 ... k-1.

Secondly, I started to think about the difference between adjacent elements, sum of triple such differences should be equal to zero. And after a little reasoning, i decided to take second set of differences as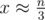 -(x+1), +x, -(x+1), +x..., so the third set will be +x, -(x+1), +x, -(x+1), where . After that, i had only to adjust the coefficients for x and the first element of the second set.

Also, there is a very simple solution with a cyclic shift. It looks like:

0 1 2 3 4 5 6 7 8
4 5 6 7 8 0 1 2 3
8 6 4 2 0 7 5 3 1

→ Reply
»
8 years ago, # |
  Vote: I like it +17 Vote: I do not like it 
#include <iostream>
using namespace std;
int main(){
	freopen("in","r",stdin);
	int n; cin>>n;
	int k = (2*n)/3;
	cout<<k+1<<endl;
	int y = 2*k-n;
	int x = n-2*y;
	for(int  i=0;i<=y;i++){
		cout<<i<<" "<<x+i<<" "<<n-x-2*i<<endl;
	}
	for(int  i=0;i<k-y;i++){
		cout<<y+i+1<<" "<<i<<" "<<n-y-1-2*i<<endl;
	}
	return 0;
}

This is why it is achievable

→ Reply