Have you ever seen a problem connected to graphs diameter, where it is used in complexity?
For example: http://main.edu.pl/en/archive/oi/21/tur .
Model solution goes O( (1 + sqrt(2)) ^ T) * (n + m) ), where n is number of vertices, m — edges and T is the longest path which we can encounter in it. However, longest path is not a diameter. I've just wanted to show what I am talking about.
Any help with finding such a problem would be highly appreciated. Thanks in advance!
If I understood right, the solution should be some biconnected components problem (you solve it with back inside a component and than big dynamic programming on the formed tree). We have 2 such tasks in Romanian "culture", both of them being well-known in our country as very hard to code problems.
Not really. It can be for example O(diameter * (n + m)) and it doesn't have to be really hard. Could you please post the link to the problems?
Ro and Santa. Sadly, i'm pretty sure the statements are available only in Romanian.
Of course, but I warn you, they are in Romanian :)) Still, google translate is always an alternative. These are the links: link1 link2 .Have you ever seen such a problem (with polynomial diameter based complexity)? Am I that wrong about the mentioned task (it is not solved with biconnected components), or you are referring at some other task (and if so, pleas provide a link :)) )?
I'm referring to my own intuition that such task may exist. But I can't come up with a good example as I don't have any!
When I asked people about problems from first day of that final many people (including well known members of jury) told me constraint that diameter is <=10. It seemed to me like pretty useless constraint, after some time my friend found in Internet that this problem is NP-hard even for diameter=2. After reading the actual description of the task I was like "all the people, WTF were you saying??!!"... There is very big difference between longest simple path in graph and its diameter. Graph consisting of a cycle on n-1 vertices and one additional vertex connected to all vertices on that cycle has diameter of length 2 and longest simple path of length n.
My butthurt has just reborn after reading first two lines of your entry, fortunately you made it clear you know the difference in next paragraph, but two-line-prefix of your post is misleading :P.
If the graph is a tree then the diameter and height are almost the same :)
Not sure if it is what you are looking for, but I'll give an example.
There was a problem in Petrozavodsk training camp last summer: Given n, let's consider a graph on n vertices numbered from 1 to n which edges have weight gcd(u, v) for edge u - v. Your task is to find a weight of maximal spanning tree of this graph. There were up to 105 tests with n up to 105.
We can consider only edges with v|u, there are
such edges. Now we will solve for all n from 1 to 105. We will add edges one by one and rebuild current spanning tree. To do so we have to find the lightest edge on the path between two vertices in a tree and then replace it with the new edge if it is heavier. This can be easily done in O(h) time where h is current height of a tree.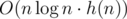
, h(n) is not big due to specific of the graph.
Total complexity will be