Problem link: Here
So I came around this problem in a practice contest and after reading the statement I thought it would be simple. But when I noticed that the cuts were to be made totally in random places (not in integer portions), I was confused how to handle this kind of problem. Then I thought that in how many ways could I NOT make a polygon. Then I noticed that the largest side must be greater than or equal to half of the length of the stick. So if I slide this portion to a side, then all the k cuts must be made on the same side of the midpoint of the stick. Thus all possible choices become 2^k. But in how many ways I can place k cuts? I thought hard and I couldn't figure it out. Then I jumped to intuition and made some guesses and cross-checked with sample cases and the answer seemed to be 1-(k+1)/2^k. I implemented it and it was Accepted. But actually I don't have a clue why this worked. Later I found online that almost every solution was similar to mine. But no clear explanation was there. There is an explanation in CSDN blog but I didn't get it as it was in Chinese. And also, there are some explanations in mathStackExchange but they are for smaller cases like k=2 or 3. I was actually looking for a nice explanation for a general value of K. Please, is there anyone who can explain this to me in simple terms? I would be really grateful. Thanks in advance.
Notice that n doesn't come into play at all.
WLOG, let n = 1.
Our answer will be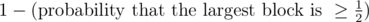
.
Let us calculate the second term. Let the cuts appear in x1, x2, ... xk.
Note that xi as written are not sorted. x1 is the first cut, x2 is the second, and so on.
Step 1. All n cuts lie in the same half — so either
for all i or 
for all i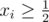. This probability is 2·2 - k.
Step 2. There is a block with size
which does not occur at the endpoints.
Let us say that this block was created with xi < xj. We will have to multiply k(k - 1) at the end, since there are k(k - 1) choices.
Now the remaining probability is k - 2 other points lying on [0, xi] or [xj, 1].
This probability is
.
Therefore, our answer is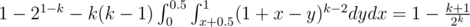
after some calculations.