
Welcome to 2016-2017 CT S03E03: Codeforces Trainings Season 3 Episode 3 - 2007-2008 ACM-ICPC, Central European Regional Contest 2007 (CERC 07). The training duration is 4.30 hours. It is opened for teams as well as for individual participants. After the end you may use the practice mode to complete problem solving. Also it will be available as a virtual contest for whose of you who can't take part today. Please, do not cheat. Only fair play!
We are planning to start on September, 21, 2016 13:10 (UTC).
It is possible that the problems will be too easy for some participants, it is possible that we will add some problems.
Good luck!











Typo in title: S03E02 (should be S03E03)
same typo is in gym page contest name too...
available*
how to register for it?
Follow this
What's wrong with the problems?
Please, help me to find a max sum of test cases in problem — A?
How to solve Problem Weird Numbers ?
I'll explain my solution, which I'm pretty sure is not optimal.
Thanks for the explanation!!! :)
I'll explain my solution, which I think is optimal.
Its almost the same as converting in positive bases. Lets convert N from base 10 to base b (b < 0):
N = a0·b0 + a1·b1 + ... + an·bn
note that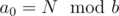 , so (N - a0) / b = a1·b0 + ... + an·bn - 1 and we can repeat recursively.
, so (N - a0) / b = a1·b0 + ... + an·bn - 1 and we can repeat recursively.
Thanks for the explanation!!! :)
Anybody knows where can I find the editorial ( :
Thanks
Why did answer "4 2 3 4" fail on the second sample? (Problem S. Robotic Sort)
It is said in statement: their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too. So you should also consider the INITIAL indexes of elements.
What is solution for problem C(Phone Cell)? We thought that problen can be solved by geometric invertion, but we don't know, how we can use it.
You can find all solutions here: Link
How to solve B? :(
Consider all the tiles of row 1. There are m tiles and 2^m ways to select a subset of them to be flipped. Notice that this uniquely determines all the other tiles which needs to be flipped to clear the billboard afterwards.
Consider cell(2,1). If cell(1,1) is on, then cell(2,1) must be flipped. And if (1,1) is off, (2,1) should not be flipped. Because after flipping (2,1), (1,1) is on and now there is no way to turn off (1,1) since the columns to be flipped in row 1 is fixed.
Complexity: O(2^m * n * m)
I used bitmask but it keeps giving me TLE on test 2, I submitted the same code on SPOJ(where time limit is 3.6sec) it got AC, How to get AC when time limit is 1sec using bitmask?
You can optimize your solution with the bitwise operation! Complexity: O(2^m * n) Here is my solution
Try all possibilities for the first row, after that it's easy to see which ones you should switch in the second row (the ones that are still black in the first row), then the same applies for the third row, etc..
We actually solved it using systems of linear equations.
Suppose aij is the number of times a tile at row i and column j gets swapped. First of all, aij ≤ 1. Then, for each position (i, j) we can get it's final color as (initial_colorij + aij + ai - 1, j + ai + 1, j + ai, j - 1 + ai, j + 1) mod 2.
That gives as a system of equations with n·m equations and unknowns. Sure it's not as easy to code, but it gives better time asymptotic.
The system of equations can have many solutions, how do you choose the one that minimizes the number of taps?
Great question!
It turns out, that number of free variables (meaning we can choose any value for them) is not that big (7 for 16x16 matrix). We can search over all possible values for this (at max 7) free values and find other unknowns, then choose one that minimises number of taps.
Can anyone explain the solution for Problem C?