I was trying to solve this problem on Codechef . Click Here
After spending a couple of hours on this I could not come up with any dp relation .
Can someone please provide a dp recurrence for this problem and help me solve it ?
Thanks in advance.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | Dominater069 | 154 |
| 8 | awoo | 154 |
| 10 | luogu_official | 150 |
I was trying to solve this problem on Codechef . Click Here
After spending a couple of hours on this I could not come up with any dp relation .
Can someone please provide a dp recurrence for this problem and help me solve it ?
Thanks in advance.
| Name |
|---|



Break free can be solved using binary search and greedy. Let us binary search on the answer, now we have to find minimum number of edges to be broken to decrease all subtree sizes to less than X. The greedy idea is to DFS the tree, and whenever a sub tree has greater than X weight, remove the edge to the heaviest children. It is easy to see why this works. Complexity is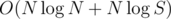 where S = max sum of tree weights(2·1013).
where S = max sum of tree weights(2·1013).