Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
| Название |
|---|



Скажите, пожалуйста, в задаче C путь может быть двусторонним? То есть случай, когда и из U есть путь к V, и из V к U. V и U — соседние вершины
Такая ситуация противоречит условию о том, что в графе нет циклов.
Спасибо за ответ! А зачем тогда в условии написано " некоторые из которых соединены односторонними дорогами"
Что это означает? Зачем слово "некоторые"?
Это означает, что не все пары достопримечательностей соединены дорогами.
Слово "некоторые" здесь для того, чтобы подчеркнуть, что граф не полный. то есть может быть случай, когда между парой вершин может НЕ быть дороги.
can anybody help me with problem C. how will i come up with such a solution...
Its actually a pretty common idea for directed acyclic graphs to run some dp on them via dfs.
Can you explain the common idea in more detail ? Please It would be very helpful for us :)
You can solve Problem C using dp on this DAG. Every DAG has Topological Orders,and we can use an order for our dp.
How do I get the idea of using topological sort for dp?
Solve problems!!! If you can't get the solution then read editorial and ask people. Try 645D - Robot Rapping Results Report it's similar idea, but more complicated because it involves some binary search.
DP has a nature that if we want to know the answer of this situation, we must be aware of the situation and answer before it. What amazing is, topological orders have the same nature. I will think about the topological order as soon as I have confirmed that the graph is a DAG.
Problem D.
I missed something or looks like you assume that the optimal sequence doesn't change a at all, that's not true.
Is it about the third part of editorial? If yes:
The sequence we consider doesn't change a because we assume that if we change a when it's minimum, we won't come to the optimal answer (and we can't change it at all after that moment because the order of operations doesn't matter). So we show that if we hadn't changed a, our answer will become worse than if we changed it, so our assumption was wrong and changing a will lead us to optimal answer.
We consider some iteration i when the element b was changed instead of a. But later operations could change a several times. The proof considers only case when a didn't change after iteration i at all.Actually I missed line about further operations. Could you explain why we we won't change a later in more details? If the order does not matter optimal sequence of changes gives us some vector (p1, p2, ..., pn), greedy solution (g1, g2, ..., gn), where pi, gi is how many times we changed the i-th element, And these two vectors differ in a and b, g[a] = p[a] + 1, g[b] = p[b] - 1.
For problem D, I couldn't grasp the editorial too easily. So I understood it on my own in the following fashion.
Let the overall product be prod = a * b.
Consider an operation on element a. |b| is max
|b| is max 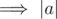 is minimum.
is minimum.
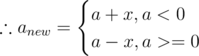
|prodnew| = |a ± x|.|b|
|prodnew| = | |prod| ± x|b| | = |anew|.|b|
So the maximum amount by which |prod| can be changed occurs when |a| is minimum. Why? Because x|b| is max
Case 1 prod is + ve:
We can either change the sign of prod to - ve or decrease prod by max amount.
This is so because if a < 0, then adding x to it will either make a ≥ 0 or it will decrease |prod| by max amount. The second condition can be derived in the same way.
Case 2 prod is - ve:
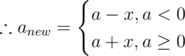
We need to increase |prod| by max value. This means making |anew| as max as possible.
Here is the AC code.
Its a good proof but needs a few clarifications to make it technically right. It's not true that the maximum decrease in |prod| occurs for min |a|. Say our set is {2, 5, 10}. Say x = 10. Clearly here a = 2 and if we decrease 2 by 10 we get the |prod| as 400 where as we would have got |prod| = 0 by choosing to decrease 10.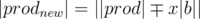 if x < = |a| then prod must decrease for which we add to a if x > |a| then changing of sign is possible hence the most new prod can be obtained by choosing a and adding x to a. We can follow similar arguments for other cases as well.
if x < = |a| then prod must decrease for which we add to a if x > |a| then changing of sign is possible hence the most new prod can be obtained by choosing a and adding x to a. We can follow similar arguments for other cases as well.
Lets build on your proof to justify why your algo works correctly. If prod is +ve: If a > = 0, if x < = a then clearly |prod| should be decreased as per the formula. if x > a , x — a will make the product most -ve hence we choose a even though |prod| may actually increase, prod we definitely decrease the most.
if a < 0 Note that the
The maximum distance by which |prod| can be moved right or left on the number line occurs when a is minimum. Ofcourse since it's absolute value, then moving it too much towards left will ultimately cross the origin and then the absolute value will increase.
My derivation of the cases is just fine.
Yeah, sure. Just wanted to make it explicit that choosing min |a| is not just based on reducing |prod|. I gave a justification as to why it should work in cases where |prod| seems to increase.
Also, this proves that this is the most optimal way for each individual update. Can you please elaborate how this necessarily implies that the end product(After k updates) is optimally small ? . I could not get the editorial in this regard.
If your current prod is - ve, then you will never change the sign. You will just increase the absolute value by making - ve more - ve and same for + ve. I have shown that for this you have to operate upon the smallest number in absolute value. This guarantees optimal solution after k operations.
If your current prod is + ve, you would try to change the sign to - ve or decrease the prod value by maximum amount. Fortunately, our solution to decrease the prod value by maximum amount is also the exact step we need to change the sign to - ve. If sign changes to - ve, you can proceed as mentioned above. If not, after applying the reqd operation |bnew| > |b|. GREEDY works like a charm!
GREEDY works like a charm!
Sure. I get that. But this is not mathematically rigorous. e.g. Lets say an algorithm choose some |b| > |a|, which does not decrease the product as choosing |a| would have done, but it could be possible that this algo takes some step later in the pipeline to compensate for this. How can we definitely say that this cannot happen ?
Brilliant solution
I have two solutions to problem E,one is the solution I used during the contest and its complexity is O(nlogn),the other one is the solution optimised to the first solution,and its complexity is O(n). Their ideas are identical and they both use dp. The O(nlogn) solution uses binary search to identify the position which needs to be transferred,and the O(n) solution takes advantage of the monotonicity.
I'm sorry that I don't know how to make hyperlinks here,so I can only provide the ID of the two codes.
O(nlogn):21041800
O(n):21104290
here are the links, thanks for your solution 21041800 21104290
:) Thank you for your help.
Can you please explain the logic behind your O(n) solution ?
The O(n) solution just replace the binary search in the function "query". You need to know the variables that the function returns is the position which needs to be transferred and it is monotonous obviously.
In fact the O(nlogn) solution has got the main idea (greedy+DP) .The O(n) solution just use a trick to optimize the O(nlogn) solution.
Maybe it implies that, for a segment, storing the maximal number of songs to sing in that segment where position as left as possible, is enough. It may require some proof though.
What you said is the meaning of f[i].
As for the proof , for a pair(a,b) (a is the maximal number of songs,b is the position as left as possible),It is clear that (a,b) is not worse than (c,d) (c<=a,d>=b).And for (e,f) (e<a,f<b), it is not better than a certain (c,d),so it is not better than (a,b).
Извините а что в задаче Д значит пока есть нули мы отн их избавляемся
пока у нас есть нули, произведение всего массива будет ноль, значит и отрицательным мы его сделать тоже не сможем. поэтому выгодно избавляться от них.
Can someone explain problem E solution? This looks pretty neat.
Can anybody explain the complexity of C-Journey??
The complexity is O(M*N) where N is vertices and M is edges. The Idea was to run dp on DAG , which can be done with dfs in general. Here is Code
Could an author's solution be provided for each problem? A link to it would be sufficient. I especially want to see solutions for C and D.
anybody know whats wrong with my D? http://codeforces.net/contest/721/submission/21054178
my solution looks the same as the editorial
Do we really have to use a reversed graph to solve problem C? Can we use the given graph and do the same stuff but starting in point 1?
No, you can do topological sorting first. See solution http://codeforces.net/contest/721/submission/21117607
We can also do it without topological sorting, with modified Bellman Ford's. My solution
Why do I need a topological sort? Why can't I do the same DP as in the official solution but starting in the first vertex?
I think you can directly do dp (for example, using dfs) on the given graph as long as you start from vertex 1 and stops at vertex N.
It's somehow similar to doing it on topological sorted vertices — you may find that your dfs won't go beyond 1 and N.
yes you can directly do dp , i.e do dfs (starting from 1 ) on each non visited vertex once and then update table, also you need not stop at vertex N . If you don't stop at N , the algo will do unnecessary calculation only and the answer won't change.check 23475069 and 23475056 . But clearly stopping at N is a better approach..
http://codeforces.net/contest/721/submission/21035009 the following submission of the second question i.e. password ,my solution got accepted in the pretests however during the system check it got a wrong answer on pretest 14 ,here the number of unsuccessful password attempts are 5 and one for correct the answer should've been 6 ,since there is a penalty after 6 wrong submissions.Could any one please explain it. Thank you
There are six words whose lengths are less than or equal to the real password, and k = 5, so there is one penalty in the worst case.
Можете пожалуйста объяснить, почему мы храним граф транспонированный граф в С?
I think problem D is simple than C.What do you think?
I don't think so. D requires more proving and is easier to write bugs. C is fairly straightforward DP, if you know what the solution might look like, although it took me 10 or more submissions ;D
Please explain solution for problem E. Its not at all clear from editorial (specially if p>100).
for p ≥ 100 , let's denote dp[i] as the minimum distance it can sing up to i songs and you are now dealing with some of the segment, let's see how it can affect the answer.
For the right point of the current segment — r, you can sing at most (r - l) / p songs, now iterate through 1 to (r - l) / p, meaning you want to sing these much songs.
Say, you want to sing j songs in this segment, then, your last songs must be sung before r - j * p - t(why not r - j * p ?).
Then, you want to find maximum i, where dp[i] ≤ r - j * p - t, meaning that you can sing at most i + j songs in this segment if you want to sing j songs in this segment, which should update dp[i + j]
However, there's another problem. Will this affect answers to dp[k + j] where k < i ? The answer is no. To illustrate this may require some efforts, but I suggest that you may compare the two cases when you are singing j songs and j - 1 songs, the key to the prove is that for any s, dp[s] - dp[s - 1] ≥ p.(This part will be tough, and I don't think I can convince you by typing here, drawing a picture may help)
Then finally, you may get code like this:
as j travel through number of songs, so it won't exceed L / p, and finding the i could take O(log(L / p)) if you use binary search. So the complexity is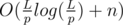
Thanks a lot! I think there is also a O(n) solution independent of size of p. (n = number of segments)
If you know..can you explain that also ?
Could anybody explain my doubt in problem D?The greedy stategy only proves that in one step we should choose a number with minimal absolute value,but why can it assure that the final answer is optimal?
For problem C. I use dp[i][t] represents the longest path from vertice i with t time. Then dp[i][t] = max{dp[j][t-edge[i][j]] + 1}. my 21225644 is WA. I don't know where is wrong.
wrong answer Path must end in vertex 1000When I first saw Problem C, I thought it can be solved using Dijkstra's. I am not exactly sure why Dijkstra's cannot be used here, since we do not have any negative edges ? Can anyone tell me why we cannot use dijkstra's ? As you can see from my submission here http://codeforces.net/contest/721/submission/21121352. The code fails for 13th test case. I know where it fails but I am not sure why though?? :(
For test 13: the input is basically:
Since (1,9) is longer than (1,2), you go through path 1-9-10 first, with total distance of 3. now par[10] = 9, par[9] = 1.
Then you try (1,2). You go all the way through 1-2-3-4-5-6-7-8-9, but you can't reach 10 because total distance from 1 to 9 is already 8. So, supposedly, you discard the path.
But what really happens is that this failed try set par[9] = 8, par[8] = 7, ..., breaking the once-correct path 1-9-10. So now we have 1-2-3-4-5-6-7-8-9 + 9-10, whose total distance is 9.
To fix this, just store par[] in the pq instead of using a global array. This way you can have a path tree instead of everybody sharing a global path record.
At first I thought your algorithm was wrong, but after some rethinking, I wonder if it's actually correct. Correct me if I'm wrong: we try longer path before shorter path, so that we don't have to layer the graph. What I'm still confused about is:
can you / how do you make sure a longer path like a-b-c-d-e-f-g-h (weight of each edge is 1 => total 7) is not "pruned" by a shorter path like a-i-h (weight of each edge is 2 => total 4)?
you may need to change len[v] <= len[u] to len[v] <= len[u] + 1 so that if there is a new path with same hops but takes less time, we take that path instead.
I don't understand why my code for C. keeps getting MLE on test 8. When I tweaked it a bit, I got WA on the same testcase.
I did a simple dp+memoization approach with an array next[i] that stores the next element after i in the optimal path.
Can anyone spot a mistake?
Your state of DP is exceeding the array bounds. You have taken (node, time) taken as state and rather it should be (node, no.ofedges). Because Time is very large here < = 109, so it cannot be a parameter for the state.
I just solved problem C using 2D Dijkstra :) 36453100
I was looking for something like this. Thanks a lot :)
Problem C: This solution $$$\to$$$ 58517982 uses neither topological sorting nor memorized dfs, but it passed. Why?
in problem C
test case :
5 6 10
2 1 1
2 3 1
1 3 1
3 5 1
4 2 1
4 3 1
you may get accepted on it, but this test does't get the correct answer
correct answer is
3
1 3 5
In C, why am i getting TLE on test case 7?? https://codeforces.net/contest/721/submission/87456309 Please Help!!!
I didn't understand why it is showing Memory Limit Exceeded on my solution. This is my solution https://codeforces.net/contest/721/submission/99400340. I only used O(n*2) space complexity. Someone help me please !!!
If you understood plz explain Cant understand why my code is giving MLE on test case 8 238429202 <-my code