Let's discuss problems.
How to solve 8? I have no idea at all and finally decided to believe that we don't need nested addition/subtraction blocks, but it got WA. It seems there are harder cases.
How to solve 12? Essentially it reduces to the following: you are given a circle C and a point P. Find the movement of a point on C whose angular velocity is proportional to the distance from P. Is numerical integration accurate enough?











8 is solved with precalc. Basically store all possible sets which you can reach in k moves and do all possible moves from each of them. With n up to 1000 answer doesn't exceed 8, and the whole backtrack works in a few minutes.
P.S. I didn't get Accepted and don't know if my solution is basically correct (forgot to add input.txt/output.txt while submitting the output in the very last minute), but the same solution by Endagorion was accepted.
How to solve 1? I have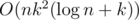 and get TL 31.
and get TL 31.
dp[type][n][k1][k2] — type is either 0 (segment hasn't started), 1 (segment is open now) or 2 (segment has already closed). k1 — number of elements that we swapped in the segment, k2 — number of elements that we swapped out of the segment.
answer is in dp[1][n][i][i] or dp[2][n][i][i]
Can you show your code, please?
The same complexity we have accepted in upsolving. We got TL31 when doing k4 instead of k3.
Our solution on 1:
Let us have an arbitrary segment [l, r] and two sets (multisets, but then we add to every number an index of it in order to recover necessary swaps for answer) of numbers on [l, r] segment: one set is for numbers
insidethe segment, one is for theoutsidenumbers. Then we can easily get a sum with swaps on [l, r]: using prefix-sums (or whatever to get an actual sum) on a [l, r], then simultaneously iterate overkbiggest numbers (from biggest to lowest) inoutsideand smallest ininside(from smallest to biggest) sets, and change our computed sum according to these values (will the sum get bigger, if we swap those values?).The solution is just to move two pointers over an array, while sustaining two sets accordingly and update answer if necessary.
Does anyone know what is wrong with this approach? We've got WA8 or something with that.
Function ans(l, r) with fixed l isn't monotonic on [l, roptimal].
As far as I understand, your solution will fail this test:
5 0
1 1 -1 1 1
Here ans(1, 3) < ans(1, 2) < ans(1, 5)
We move r pointer until ans(l, r) becomes negative (I think it is obvious why should we look after negative sum, but I could be wrong) — than we set l = r and go on.
My solution produces
3 0
1 5
on your test-case.
6 1
1 -1 -1 2 2 -5
Optimal answer is segment [3, 5] or [2, 4] with negative number swapped out. On the other hand, ans(1, r) isn't negative for r < 6. So your solution will skip segments with l = 3 and l = 4.
Oh, right, many thanks for an explanation!
8 can be solved with bruteforce with pruning from fixed starting set of powers of 2 in less than 100ms.
Как решать 10? И почему не работают 2 медианы (по Х и по Y) и выравнивание жадным способом вдоль прямой, проходящей через них? (wa40). И как решать 7?
В 7 поток. В одной доле матчи, в другой команды. В каждый матч входит три очка, из каждого матча два ребра в соответствующие команды, и из каждой команды выходит столько, сколько осталось команде набрать. В принципе, так как пропускные способности не большие, с помощью дублирования вершин можно и к парсочу свести (но это бессмысленно =)).
Работает такое решение: сортируем по X, вычитаем из каждого X его индекс в отсортированной последовательности и находим медианы по X и Y. (И аналогично поменяв местами координаты)
Смотря как выравниваешь. Рассмотрим стартовую точку на линии, пусть это будет L. Тогда все кубики будут располагаться от L до L + n — 1. Будем жадно двигать, то есть, самый первый кубик в L, второй в L + 1, i-тый в (L + i — 1). Несложно заметить, что при таком поставлении, L будет равна медиане среди a[i] — i + 1.
I am also interested in solution for Problem 12. I tried to solve it and I think I did everythin right, but the output numbers were a bit different from the example output. I have no idea on what went wrong, looks like some kind of computational error. Here is my code. If you want I can explain it, but actually it is not the right solution. If someone can explain how to solve this problem, I would appreciate that.
It's not true, that angle speed is equal all time. You losses part of speed v to go along line.
Oh, I got your point, thanks! And thank you for explanation below.
In 12 i got ok with following.
Let φ(t) be the angle you are talking about (counted from vector u as zero).
Then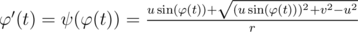 .
.
Now, we can get time ti when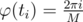 . It's can be calculated as
. It's can be calculated as 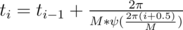
Now, if we get time t, φ(t) is close enough to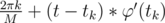 , where k is smallest where tk > t (we should shift t to range [0, tM] before this).
, where k is smallest where tk > t (we should shift t to range [0, tM] before this).
With M = 3·107 it gets OK in YandexContest.
Can you please explain a little bit more?
Which part? When we know, how to get derivative from angle, it's just numerical solving of differential equation.
To get equestion, we considering x(t) = x0 + ux * t + r * cos(φ(t)), y(t) = y0 + ux * t + r * sin(φ(t)) (this is because distance is constant), and just simplify x'(t)2 + y'(t)2 = v2 (which is condition given in statment). This is square equation on φ'(t), which gives forumla above. I don't really ready print all counting here.
Thanks, it is much clear now. Quite interesting to see stepping on perimeter instead of time. Although from mathematical point of view, it is more sensible to step on perimeter (otherwise, big step != circle).
Well, i got TL2, tring to step on perimeter. We have derivatives which are not to small, and not to big, so probably both have same order of error. And i didn't make more precise analisis.
Как решать 5 6 7 9 10 11?)
5) Сгруппируем строки из словаря по равенству без учета регистра. Для каждой строки из ввода заведём битовый массив: 1 -- верхний регистр, 0 -- нижний. Количество различных бит можно посчитать с помощью ксора и __builtin_popcount. Получается O(n·q·L / 64). Работает полсекунды.
6) Посчитаем количество чисел во вводе с каждым остатком от деления на семь. Дальше переберем число ai, которое будет представлять младшие разряды и все остатки. Прибавим к ответу количество чисел aj для которых справедливо . Не забудем что нельзя выбирать пару из одного и того же числа.
. Не забудем что нельзя выбирать пару из одного и того же числа.
Can you give me a hint for 5 and 10? Thanks!
10) Let's try to make a horizontal line (vertical one can be done similarly). Suppose, we will make a line at y = Y. Then we know the total amount of movements to bring all the points to y = Y (which is sum of |Y — yi|). Movement of x is independent of y movement. So we can minimize x/y independently. To minimize sum of |Y — yi| we should choose median(yi).
Now, let's calculate movement of x. Sort all x. It is okay to say that, x0 will be leftmost, then x1, then x2 ... Say xi moves to x = i. Then signed movement is: set(xi — i). Let, xm = median(set(xi — i)). Then, you have to move: xi to i — xm. Why? Can be proved, can't find are simpler argument now.
5) I got tle by suffix array. Later got ac using hashing+bitset. For each word, I converted the word to lower case and computed hash value (some simple polynomial hash). Also I kept a bitset consisting of 0 for lower case, 1 for upper case (AbaC = 1001) Then for each (word, query) I checked if they satisfy all the conditions (length equal, hash same, count of ON bits in xor of bitset <= K).
There's no need in hashing — u can jsut sort input and find words which are same in lowerace with query via binsearch
map <string, vector >
gr8 m8
Could somebody send screenshot of top-10 results of the teams that are not currently in opencup table?
For multiplier problem, the minimal case when nested blocks are necessary is N = 22 (test #5): Picture
Does anyone have tests for problem 4 that can help with WA2?
When I had WA2 these tests were useful:
This input should help you:
Can you describe the solution please?
First of all, we translate coordinate origin into the evac point and split everything into four quadrants (splitting some roads in process). Each quadrant can be solved separately, so it is enough to show how to solve the positive one (x,y > 0).
In the positive quadrant we can determine locally problematic points: there is nowhere to run from such points. They are the endpoints of the roads having no incident road leading to lower X or Y coordinate. Now we have to build a tunnel from each such problematic point to any point on road/evac which is located strictly closer to evac. if we do that, there would be no locally problematic points as the result, so clearly it would become possible to get to evac from everywhere. Also it is worth mentioning that each problematic point can be solved completely independent of the others, so length of each tunnel should be minimized.
For each problematic point (x0, y0), we have to find the closest point (x, y) on road/evac given that x <= x0 and y <= y0, and simply build a tunnel (x, y) -> (x0, y0). Here "closest" is in sense of Manhattan distance, because we can only build axis-aligned roads. Such "closest" point is equivalent to point with maximum (x+y).
Now there are two cases:
We can run vertically or horizontally (i.e. x = x0 or y = y0). In such case point (x, y) may be located in the middle of some road. We can solve each subcase by simple sweep-line algorithm. E.g. for horizontal runs we maintain X-coordinates of all vertical roads intersecting with current horizontal sweep-line in a sorted tree, which makes it possible to quickly find closest-to-the-left vertical road for any point.
We can run to a point with x < x0 and y < y0. Obviously, such a point has to be endpoint of some road in order to be optimal. This can be solved by yet another sweep-line algorithm, e.g. by moving a vertical sweep-line to right. The points already met should be stored in Range-Maximum-Query data structure with key corresponding to compressed Y coordinate of a point, and value corresponding to uncompressed (X+Y) sum which we want to maximize. Then we can quickly find a point with maximum value among those with y < y0 at any moment. In fact, Fenwick tree on maximum can be used here instead of full RMQ tree. Also, it is possible to use hand-made sorted-tree (e.g. treap) with maximums without any coordinate compression (instead of RMQ + compression), but that seems too complicated for this problem.
This results in O(NlogN) solution. Also it is worth noting that quadrant splitting should be done carefully. If a road is split into two quarters, the point of split is locally problematic and can case lots of trouble.
Thank you. I couldn't find a good test yesterday, so I wrote a slow solution that got TL17 and substituted it with the fast one part at a time until it got WA2. This way I found where the bug was :)
Does anyone have deterministic solution for problem 9 ?
First, print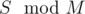 . Then we print a1 + a2 and get
. Then we print a1 + a2 and get  . Then we print a3 + a4 and get
. Then we print a3 + a4 and get 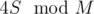 . When the new answer tk + 1 is less than the previous one tk we know that M = 2tk - tk + 1.
. When the new answer tk + 1 is less than the previous one tk we know that M = 2tk - tk + 1.
0200 times. Then denote the sum of last n - 1 elements (denote them by a1, a2, ..., an - 1) by S. We print0and getThe only problem is when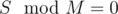 . In this case we print a1 + a2 ± 1 (plus or minus depends on if a1 + a2 equals 1e9 or doesn't) and continue in the same manner.
. In this case we print a1 + a2 ± 1 (plus or minus depends on if a1 + a2 equals 1e9 or doesn't) and continue in the same manner.
First 200 zeroes are needed in order to have a2k - 1 + a2k no more than 1e9.
Sorry, this was wrong.
Random solution is better =) Print 10 random numbers, then answer will be GCD({realSumi - responsei})
I got WA 45 on this. But tried only once, at last minute:)
First print
10^9. We will getr.(SumOfLast(n) - r) % m == 0,(SumOfLast(n) - r) > 0.Assume that we know that
m1:m1 % m == 0,m1 > 0.Let's
x = min(m1 - 1 - SumOfLast(n - 1) % m1, 10^9);r1 = SumOfLast(n - 1) % m1 + x.Let's print
xand get answerr. Ifr == r1, thenm == m1.Else if
m1New = gcd(m1, r1 - r), thenm1New % m == 0,m1New <= m1 / 2andm1New > 0.Let's
m1 = m1New. Continue this, whilem1is decreasing.At most 40 questions (first
m1 < 10^11).who can help with Problem 2. Inspection?
The round-trip doesn't have to pass through all the cities so it suffices just to find one cycle in a graph. This can be done by doing a DFS and keeping track of the current stack of vertexes.
If you cannot find a cycle then you can add a single edge to road with 2 vertexes. The possible answers can be -1, 0, 1, 2.
How to solve 11